set y = f(x) to get:
y = x^3 - 7
solve for x.
add 7 to both sides of the equation to get y + 7 = x^3
raise both sides of the equation to the power of (1/3) to get:
(y+7)^(1/3) = (x^3)^(1/3)
if a = b, then b = a, so you can flip the equation to get:
(x^3)^(1/3) = (y+7)^(1/3)
since (x^a)^b) = x^(a*b), your equation becomes:
x^(3*(1/3)) = (y+7)^(1/3) which becomes:
x = (y+7)^(1/3)
replace the x with y and the y with x to get:
y = (x+7)^(1/3)
that's your inverse equation.
let f^(-1)(x) = your new y and you get:
f^(-1)(x) = (x+7)^(1/3)
your original equation is f(x) = x^3 - 7
your inverse equation is f^(-1)(x) = (x+7)^(1/3
to prove it's an inverse, we take any value of x and solve for f(x).
if x = 9, then f(x) = (9)^3 - 7 = 722.
In our inverse equation, we let x = 722 which was f(x) in our original equation.
our inverse equation becomes (722 + 7)^(1/3 = 729^(1/3) = 9
x = 9 and f(x) = 722 in our original equation
x = 722 and f(-1)(x) = 9 in our inverse equation.
our inverse equation is good because it undoes what our original equation did.
the graph of both equations is shown below:
I was not able to properly graph the equation of (x+7)^(1/3) when x is less than -7 using the built in graphing algorithm of algebra.com.
that piece is missing.
the following picture of another graph of the same equations shows you what it should look like.
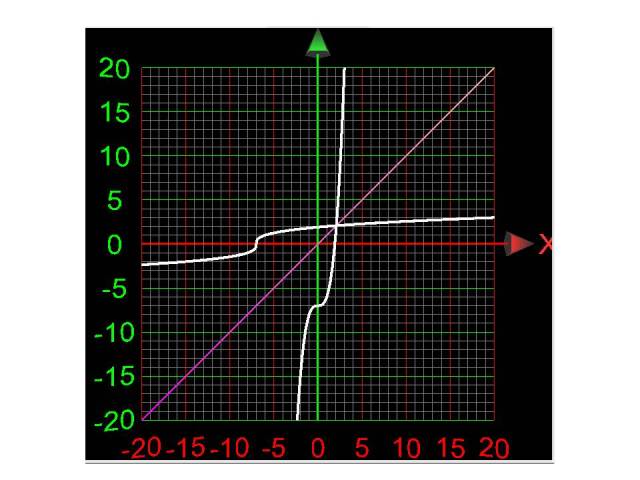
since the graphs are inverse functions, they show up as reflections about the line y = x.