SOLUTION: At a price of $70 for a blender, Home Outfitters will sell 12 in one month. Market research has shown that for every $5 decrease in the price of a blender, they will be able to se

Question 1203126: At a price of $70 for a blender, Home Outfitters will sell 12 in one month. Market research has shown that for every $5 decrease in the price of a blender, they will be able to sell 3 more each month.
a) Determine the price of a blender that will maximize revenue for the month.
b) Approximately how many blenders will be sold to reach revenue of $1100?

Found 2 solutions by ikleyn, Theo:
Answer by ikleyn(52778)   (Show Source): You can put this solution on YOUR website!
.
At a price of $70 for a blender, Home Outfitters will sell 12 in one month.
Market research has shown that for every $5 decrease in the price of a blender,
they will be able to sell 3 more each month.
(a) Determine the price of a blender that will maximize revenue for the month.
(b) Approximately how many blenders will be sold to reach revenue of $1100?
~~~~~~~~~~~~~~~~~~~~

                    Solution for (a)

From the given information, we easily derive that 12+3n blenders can be sold at market at the price 70-5n dollars, where n is "any" integer number, meaning n steps of $5 decrease the initial price of $70. Hence, the formula for revenue selling blenders at the price 70-5n dollars is R(70-5n) = (70-5n)*(12+3n) dollars. We want to find the value of the argument 70-5n, which provides the maximum to the quadratic function (70-5n)*(12+3n). For it, notice that the quadratic function (70-5n)*(12+3n), just being decomposed into the product of linear terms, has the zeroes (= x-intecepts) at = 14 and = -4. Thus it has the maximum half-way between the x-intercepts. This half-way value is = = = 5. So, to get an optimum price, we need to make 5 steps decreasing the initial price of $70 by $5 each time. Thus we get the optimum price of 70-5*5 = 70-25 = 45 dollars. At this price, 12+3n = 12+3*5 = 12+15 = 27 blenders can be solved, providing the maximum possible revenue of 45*27 = 1215 dollars. Compare it with the revenue of 12*70 = 840 dollars, corresponding to the initial condition.

Part (a) is solved.

                    Solution for (b)

To answer (b), we should find integer values n that provide the closest values of (70-5n)*(12+3n) to 1100. To get it, I used MS Excel and prepared this Table below n 70-5n 12+3n product (70-5n)*(12+3n) --------------------------------- 1 65 15 975 2 60 18 1080 <<<---=== 3 55 21 1155 4 50 24 1200 5 45 27 1215 6 40 30 1200 7 35 33 1155 8 30 36 1080 <<<---=== 9 25 39 975 10 20 42 840 The desired values of n are n= 2 and n= 8. The corresponding prices per blender are 70-5*2 = 60 dollars or 70-5*8 = 30 dollars (two possible values). The corresponding amounts of blenders sold are 12+3*2 = 18 or 12+3*8 = 36 (two possible values).

Solved in full.

Answer by Theo(13342)   (Show Source): You can put this solution on YOUR website!
revenue = price * quantity sold
when price = 70, quantity = 12 making revenue = 70 * 12 = 840.
when the price decreases by 5 dollars, the quantity sold increased by 3 dollars.
let x equal the number of times the price decreases and the quantity increases.
the equation becomes revenue = (70 - 5x) * (12 + 3x)
when x = 0, revenue = 70 * 12 = 840
when x = 1, revenue = 65 * 15 = 975
when x = 2, revenue = 60 * 18 = 1080
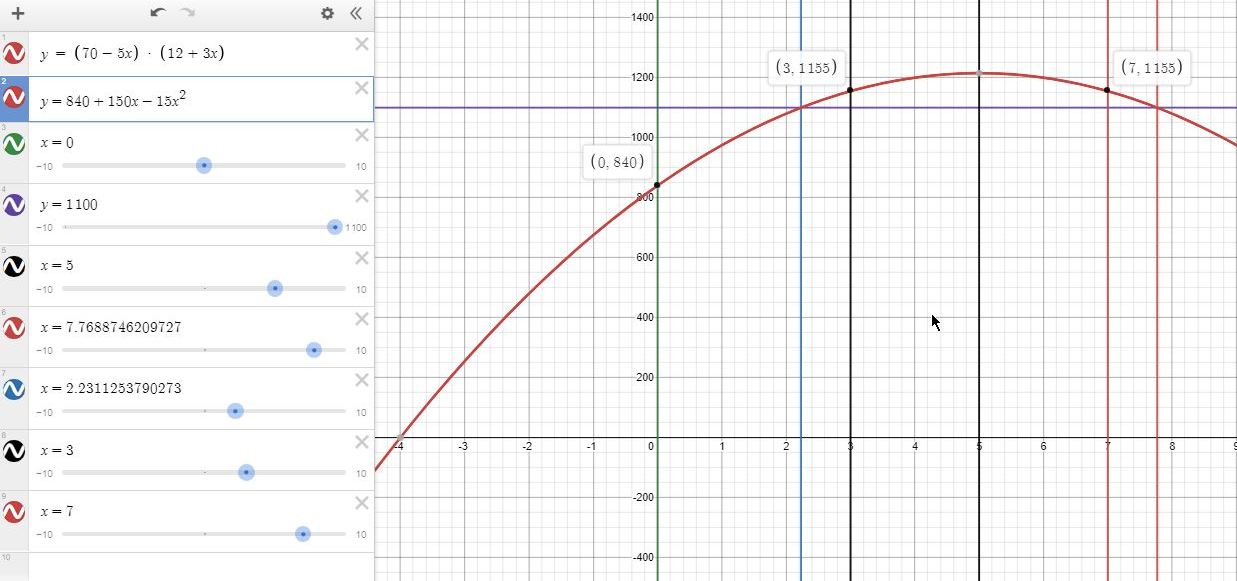
when x = 3, revenue = 55 * 21 = 1155

your revenue equation is y = (70 - 5x) * (12 + 3x).
simpiify to get y = 840 + 150x - 15x^2.
rearrange by descending order of degree to get -15x^2 + 150x + 840.

for the revenue to be equal to 1100, the equaton becomes:
-15x^2 + 150x + 840 = 1100
subtract 1100 from both sides of the equation to get -15x^2 + 150x + 840 -1100 = 0.
combine like terms to get -15x^2 + 150x - 260 = 0.
multiply both sides of the equation by -1 to get 15x^2 - 150x + 260 = 0.
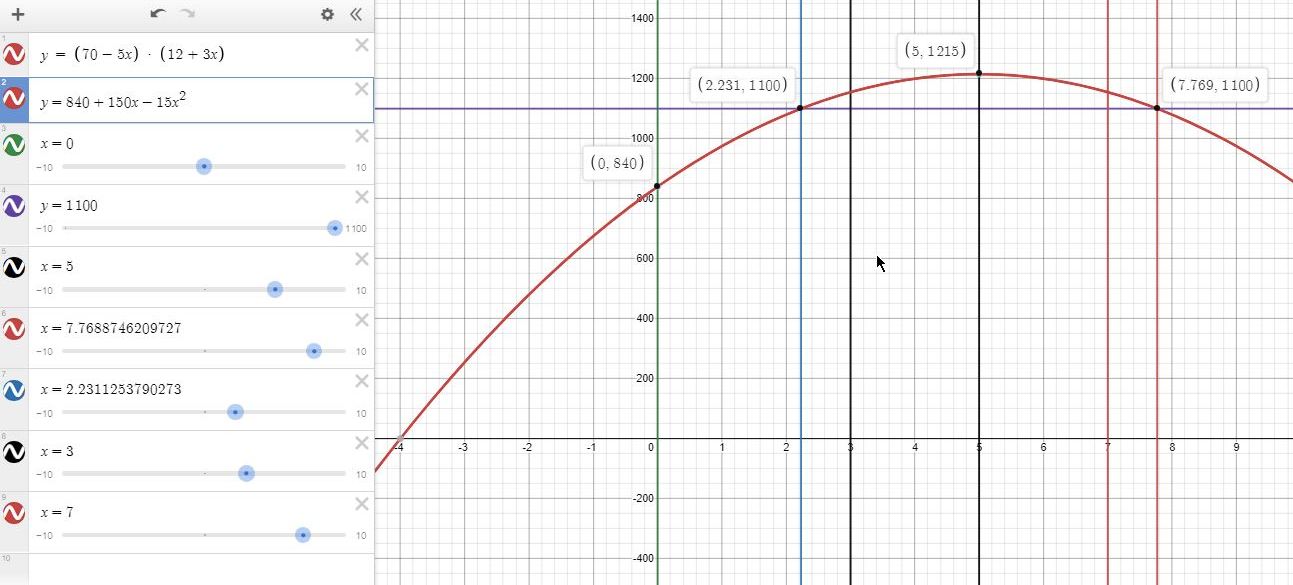
factor the equation to get x = 7.7688746209727 or x = 2.2311253790273.

your original equation is y = -15x^2 + 150x + 840
the general form of this equation is y = ax^2 + bx + c.
y will be maximum when x = -b/(2a) = -150/-30 = 5.
when x = 5, y = -15*5^2 + 150*5 + 840 = 1215.
that's the maximum revenue.
it occurs when the price is 70 - 5*5 = 45 and the number of blenders sold is 12 + 5*3 = 27.
45 * 27 = max revenue of 1215.
this is shown on the graph at the point (5,1215).
the value of x is 5 for the maximum revenue.
this means 5 increments of 5 dollars less for the price and 5 increments of 3 units more for the quantity.

the number of increments is not an integer when you want the revenue to be exactly 1100.
the values of x that allow a revenue of at or above 1100 are 2.2311253790273 <= x <= 7.7688746209727.
if you want to make the increments integer, then you would choose x = 3 to 7.
that would make the revenue greater than 1100.

here are two displays of the graph and one display of the spreadshee i used to make the calculations.

i'll be available to answer any questions you might have.
theo
RELATED QUESTIONS
A bakery has created a new type of donut that is driving the competition out of the... (answered by ikleyn)
A soccer stadium holds 31,000 spectators. With a ticket price of $11, the average... (answered by Theo)
1. In this problem, we will analyze the profit found for sales of decorative tiles. A... (answered by jim_thompson5910)
1. In this problem, we will analyze the profit found for sales of decorative tiles. A... (answered by stanbon)
1. In this problem, we will analyze the profit found for sales of decorative tiles. A... (answered by solver91311)
Suppose a market research company finds that at p=$20, they would sell x=42 tiles each... (answered by josmiceli)
a. Suppose that a market research company finds that at a price of p = $20, they would... (answered by stanbon)
a. Suppose that a market research company finds that at a price of p = $20, they would... (answered by MissionPossible)
a. Suppose that a market research company finds that at a price of p = $20, they would... (answered by Theo)