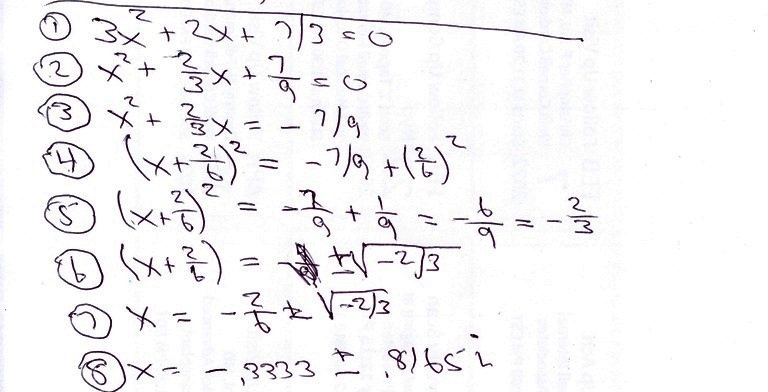
step 1 was just copying down the equation.
step 2 was dividing both sides of the equation by 3 to make the coefficient of the x^2 term equal to 1.
step 3 was subtracting 7/9 from both sides of the equation to get the constant term on the right side of the equation.
step 4 is where the magic occurs.
the equation at the start of this step is x^2 + 2/3 * x = -7/9.
you take the square root of the x^2 term and 1/2 the coefficient of the 2/3 * x term to get:
(x + 2/6)^2 - (2/6)^2 = -7/9
the reason you are subtracting (2/6)^2 is because:
(x + 2/6)^2 is equal to x^2 + (4/6)x + (2/6)^2
since you only want x^2 + (4/6)x, you need to subtract (2/6)^2 to get:
(x + 2/6)^2 = x^2 + (4/6)x + (2/6)^2 - (2/6)^2 which cancels out the (2/6)^2 so you are left with:
(x^2 + 2/6)^2 - (2/6)^2 = x^2 + (4/6)x.
you then add (2/6)^2 to both sides of the equation to get:
(x + 2/6)^2 = -7/9 + (2/6)^2
that's the equation you see in step 4, which was the result of what i showed you above.
the instructions you will most likely see would be:
x^2 + (2/6)x = -7/9 becomes:
(x + 2/3)^2 = -7/9 + (2/6)^2
step 5 simplifies the equation as shown below:
(x + 2/6)^2 = -7/9 + (2/6)^2 becomes:
(x + 2/6)^2 = -7/9 + 4/36 which becomes:
(x + 2/6)^2 = -7/9 + 1/9 which becomes:
(x + 2/6)^2 = -6/9 which becomes:
(x + 2/6)^2 = -2/3
step 6 take the square root of both sides of the equation to get:
(x + 2/6)^2 = -2/3 becomes:
x + 2/6 = plus or minus sqrt(-2/3)
step 7 subtracts 2/6 from both sides of the equation to get:
x = -2/6 plus or minus sqrt(-2/3)
since sqrt(-2/3) is equal to sqrt(2/3 * -1) which is equal to sqrt(2/3) * sqrt(-1), and since sqrt(-1) is equal to i, your answer becomes;
x = -2/6 plus or minus sqrt(2/3) * i.
that's your answer before converting everything to decimal.
if they want the answer in that form, you're done.
if they neet it to be in decimal format, then:
step 7 converts x = -2/6 plus or minus sqrt(-2/3) to:
x = -.3333 plus or minus .8165 * i, when rounded to 4 decimal places.
i checked with an online quadratic equation solver at .
it gave me the same answer, confirming that i did it right, as shown below:
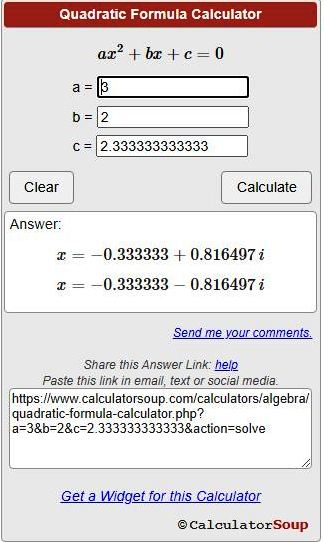
their answer not rounded to 4 decimal places.
it is a more complete answer, probably rounded to 6 decimal places..
you may round it as required.
here's a reference on how to solve a quadratic equation by completing the square.
https://www.purplemath.com/modules/sqrquad.htm
let me know if you have any questions.
theo