SOLUTION: Solving using the quadratic formula. 7x(x+2)+5=3x(x+1) Do you first subtract the 3x^2 from 7x^2? I'm not 100% on how to work this through.

Algebra.Com
Question 1027817: Solving using the quadratic formula.
7x(x+2)+5=3x(x+1)
Do you first subtract the 3x^2 from 7x^2? I'm not 100% on how to work this through.
Found 3 solutions by Cromlix, Theo, MathTherapy:
Answer by Cromlix(4381)   (Show Source): You can put this solution on YOUR website!
Hi there,
7x(x+2)+5=3x(x+1)
7x^2 + 14x + 5 = 3x^2 + 3x
7x^2 - 3x^2 + 14x - 3x + 5 + 0
4x^2 + 11x + 5 = 0
Solve using:-

a = 4, b = 11 and c = 5



:
x = -0.575 x = -2.175 (2 decimal places)
Hope this helps :-)
Answer by Theo(13342)   (Show Source): You can put this solution on YOUR website!
you want to get the quadratic equation into standard form first.

that form is ax^2 + bx + c = 0

a is the coefficient of the x^2 term.
b is the coefficient of the x term.
c is the constant term.

your equation is:

7x(x+2)+5=3x(x+1)

simplify by performing the operations indicated to get:

7x^2 + 14x = 3x^2 + 3x

not subtract all the terms on the right hand side from both sides of the equation to get:

7x^2 + 14x - 3x^2 - 3x = 0

now combine like terms to get:

4x^2 + 11x = 0

it is now in standard form of ax^2 + bx + c = 0

a = 4
b = 11
c = 0

now you can use the quadratic formula of x = (-b plus or minus sqrt(b^2-4ac)/(2a).

that will get you x = 0 or x = -22/8 which can be simplified to x = -11/4.

the graph of the resulting equation confirms that, as shown below:

$$$

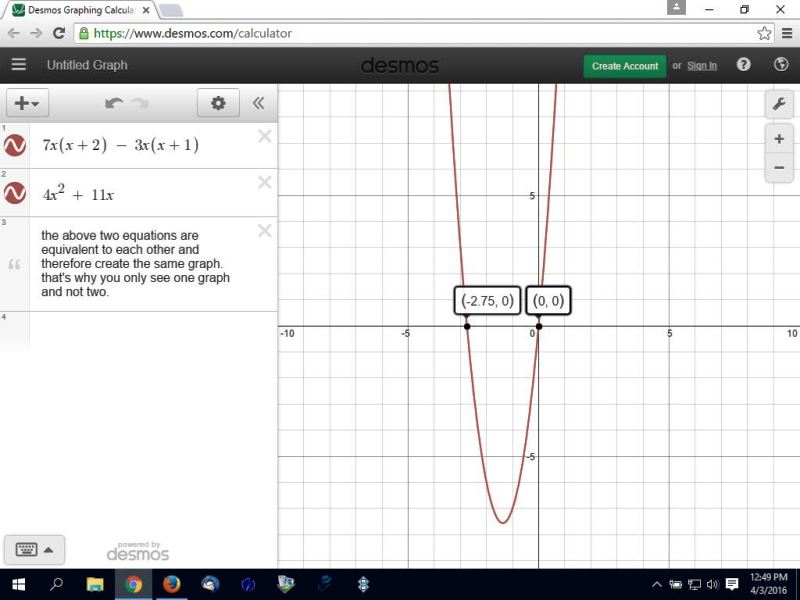
the decimal equivalent of -11/4 is -2.75, as shown on the graph.


Answer by MathTherapy(10551)   (Show Source): You can put this solution on YOUR website!

Solving using the quadratic formula.
7x(x+2)+5=3x(x+1)
Do you first subtract the 3x^2 from 7x^2? I'm not 100% on how to work this through.
7x(x + 2) + 5 = 3x(x + 1)

 -------- Distributing

 ----- Subtracting  from each side, as you surmised



Solve using the quadratic equation formula, as instructed.

a = 4

b = 11

c = 5 

RELATED QUESTIONS


Solve using the quadratic formula:

x^2 - 3x = 7x -... (answered by Fombitz)

Solve using the quadratic formula:
x^2 – 3x = 7x – 2

 (answered by jim_thompson5910)

Solve using the quadratic formula:
x^2 – 3x = 7x – 2
 (answered by nerdybill)

Hello! I've tried solving this problem multiple times but I'm not sure if I've gotten the  (answered by Alan3354,ikleyn)

I need to solve for x on the following equations. I honestly don't know what to do.... (answered by fcabanski)

Solve using the quadratic formula:... (answered by checkley71)

Solve using the quadratic formula:
x^2 – 7x – 1 = -7
 (answered by jim_thompson5910)

Please explain to me exactly how to add and subtract polynomials. Ex: x^2+5;3x^2+9 or... (answered by sdjackson71)

Solve using the quadratic formula.

3x^2-7x+3=0
 (answered by richwmiller,Alan3354,stanbon)