the equation in that problem was f(x) = 1 / (x^2 - 2x - 3).
the equation in this problem is f(x) = 1 / sqrt(x^2 - 2x - 3)).
that changes the range of f(x) because the domain is now different.
the equation we want to solve for is f(x).
we'll call the equation inside the square root sign g(x).
we'll call the square root of the equation inside the square root sign h(x).
what you get is:
f(x) = 1 / h(x), where h(x) = sqrt(g(x)) and g(x) = x^2 - 2x - 3.
put them all together and what you get is f(x) = 1 / sqrt(x^2 - 2x - 3).
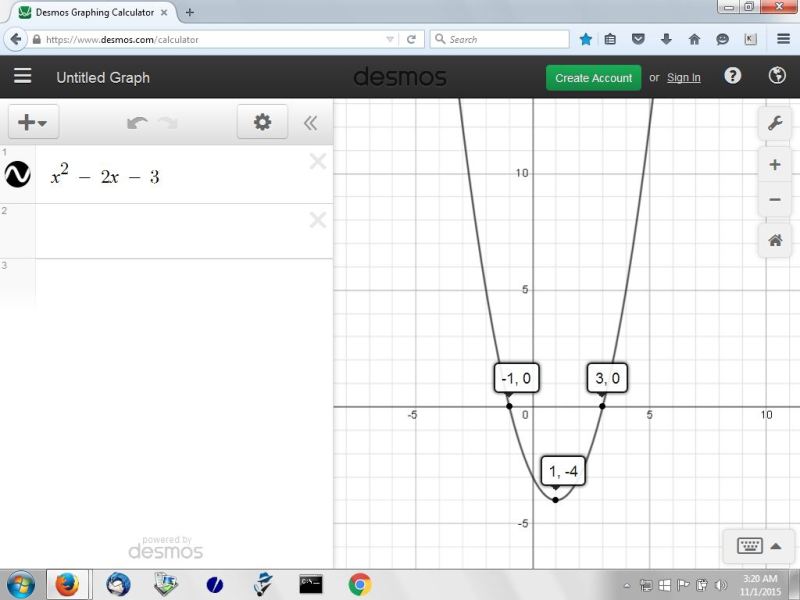
we'll start with g(x) = x^2 - 2x - 3
that can be factored to get g(x) = (x-3) * (x+1)
the function g(x) is there equal to 0 when x = -1 and x = 3.
the domain of g(x) is equal to all real values of x.
there are no restrictions.
the range of g(x) is equal to all real values of y >= -4.
y has to be >= -4 beccause that is the minimum value of g(x).
the graph of g(x) is shown below:
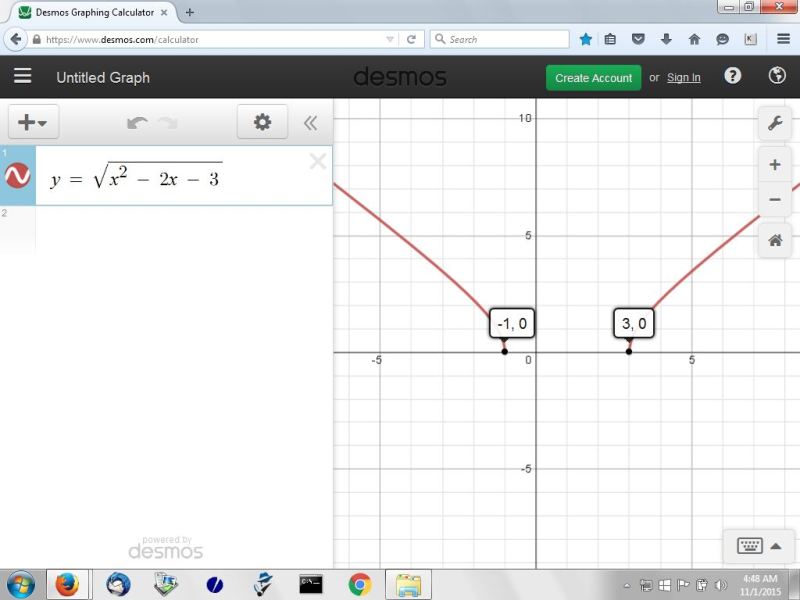
now we'll go to h(x).
h(x) = sqrt(g(x)) = sqrt(x^2 - 2x - 3).
after factoring of g(x), we get:
h(x) = sqrt(g(x)) = sqrt((x-3)*(x+1)).
h(x) will be positive if x > 3.
h(x) will also be positive if x < -1, but that is not as clear as when x > 3.
let's look at what happens.
when x > 3, (x-3)*(x+1) becomes positive because both (x-3) and (x+1) are positive.
when x < -1, (x-3)*(x+1) becomes positive because both (x-3) and (x+1) are negative and a negative times a negative is positive.
between x > -1 and x < 3, the product will be negative because (x-3) will be negative and (x+1) will be positive and a negative times a positive is negative.
so your domain of h(x) will be all real values of x >= 3 and <= -1.
the range of h(x) will be all real values of y >= 0.
the range does not go down to -4 now because the values of x from x < 3 to x > -1 are not valid anymore because g(x) is now enclosed within the square root sign.
the graph of h(x) is shown below:
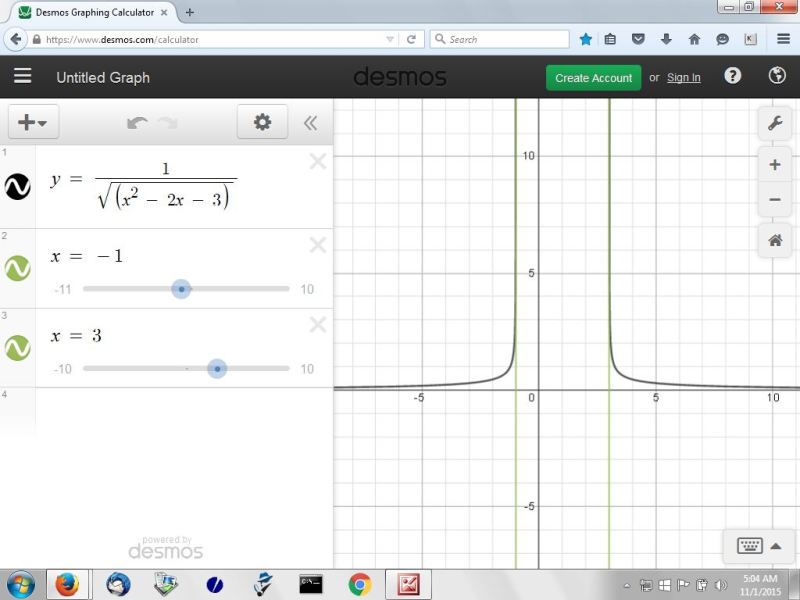
what happens to f(x)?
f(x) = 1 / h(x) which is equal to 1 / sqrt(x^2 - 2x - 3).
x can't be 3 and x can't be -1 because then the denominator will be equal to 0.
x can't be > -1 and x can't be < 3 because than the denominator will not be real because of the square root function.
the domain of f(x) is therefore all real values of x < -1 and all real values of x > 3.
within those intervals, f(x) is the reciprocal of h(x) because f(x) = 1 / h(x) which is the same as f(x) = 1 / sqrt(x^2 - 2x - 3).
f(x) is therefore equal to the reciprocal of h(x) when x < -1 and when x > 3 only.
the graph of f(x) is shown below:
the range of f(x) is all real values of x > 0.
you don't have any negative values of f(x) because the domain of f(x) does not includ any values of x > -1 or < 3.
since the domain is not valid there, you can have no corresponding values of y within that interval.