SOLUTION: I need help please, here is the problem: The costs $C of making a school bag is partly constant and partly varies inversely as the total number N of bags made. When 200 bags are

Question 1172719: I need help please, here is the problem:
The costs $C of making a school bag is partly constant and partly varies inversely as the total number N of bags made. When 200 bags are made, the cost per bag is $60. When 500 bags are made, the cost per bag is
$45. How many bags are made if the cost per bag is $40? Find the cost per bag if 400 bags are made.
Found 3 solutions by Solver92311, Theo, ikleyn:
Answer by Solver92311(821)   (Show Source): You can put this solution on YOUR website!

You are given two points on the graph of a straight line, namely and .

Use the Two-Point form of an equation of a line:

where and are the two given points to write an equation of the straight line.

Then substitute $40 for and solve for to get the answer to your first question, and then substitute 400 for and solve for to answer your second question.

John

My calculator said it, I believe it, that settles it

From
I > Ø

Answer by Theo(13342)   (Show Source): You can put this solution on YOUR website!
i could be wrong, but i believe this involves a straight line equation.
the general form of the straight line equation is y = mx + b.
m is the slope.
b is the y-intercept.
first find the slope.
you have two points.
they are (200,60) and (500,45)
the points are in (x,y) format.
x is the number of bags made and y is the cost per bag.
m is equal to the change in y divided by the change in x.
m = (45 - 60) / (500 - 200) = -15/300 = -1/20 = -.05
the general equation becomes y = -.05 * x + b
to solve for b, replace x and y with the value from either point.
i chose (200,60)
y = -.05 * x + b becomes 60 = -.05 * 200 + b
solve for b to get b = 60 + 10 = 70
the equation becomes y = -.05 * x + 70
using this equation, .....
when x = 200, y = -.05 * 200 + 70 = 60
when x = 500, y = -.05 * 500 + 70 = 45
when x = 400, y = -.05 * 400 + 70 = 50
when y = 40, the equation becomes 40 = -.05 * x + 70
subtract 70 from both sides of the equation to get -30 = -.05 * x
solve for x to get x = -30 / -.05 = 600
the graph of that equation is shown below.

Answer by ikleyn(52781)   (Show Source): You can put this solution on YOUR website!
.
The costs $C of making a school bag is partly constant and partly varies inversely as the total number N of bags made.
When 200 bags are made, the cost per bag is $60. When 500 bags are made, the cost per bag is $45.
How many bags are made if the cost per bag is $40? Find the cost per bag if 400 bags are made.
~~~~~~~~~~~~~~~~~

The problem's formulation is TERRIBLE (!)

This language was in use at parish country schools of the before-Shakespearean times
and was totally changed and replaced starting from post-Newtonian era.

Now nobody understands this language --- the proofs are the posts of the two other English-speaking tutors.

The meaning of this post (if translate it to the contemporary English) is THIS :

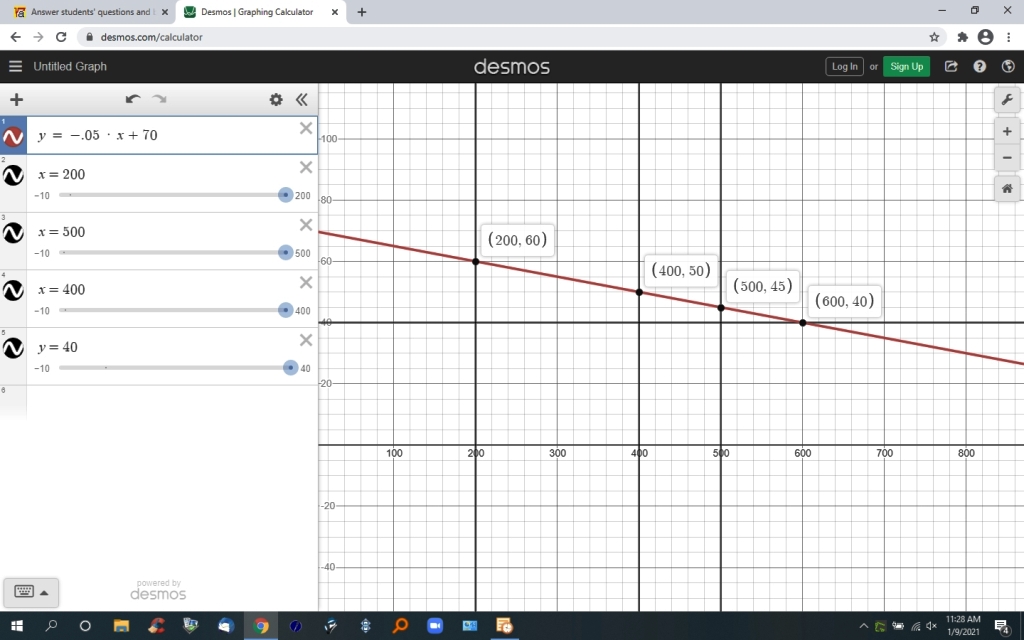
Consider the function C(N) = A + (B/N), where "A" and "B" are constants, whose values are not known now. Given : C(200) = 60 dollars, C(500) = 45 dollars. Find N, if C(N) = 40 dollars.

OK, now I will start based on my re-formulation.

At N = 200, we have this equation = 60 dollars (1) At N = 500, we have this equation = 45 dollars (2) Subtracting equation (2) from equation (1), you get - = 60-45 = 15 Multiply both sides by 1000. You will get 5B - 2B = 15000, 3B = 15000 B = 15000/3 = 5000. Then from (2) = 45, or A + 10 = 45 A = 45 - 10 = 35. To complete the solution, you need find N from the equation C(N) = 40, or = 40. The last equation gives = 40-35 = 5 N = = 1000. ANSWER. N = 1000.

Solved, answered, explained and completed.

RELATED QUESTIONS
The cost of making a dress is partly constant and partly varies with the amount of time... (answered by josmiceli)
z is partly constant and partly varies directly as x. When x=8, z=59. when x=11, z=80.... (answered by josgarithmetic)
the cost of sewing a set of suits is partly constant and partly varies with the amount of (answered by Alan3354)
a quantity c partly varies directly as d and partly varies inversely as a constant. When... (answered by ikleyn)
c partly varies directly as d and partly varies inversely as a constant. When d=4, c=17.... (answered by ikleyn)
A varies partly as B and partly C. When A=4, B=2 and C=-2, and when A=3, B=3 and C=1.5.... (answered by solver91311)
Y is partly constant and partly varies as x when x=2,y=5 and when x=3,y=10 find the... (answered by MathLover1)
D is partly constant and partly varies with V. When V = 40, D = 150 and when V = 54, D =... (answered by josgarithmetic)
The cost of sinking a well x meter deep varies partly as x and partly as the square of x. (answered by Theo)