Question 1057243: 5 men are hired to complete a certain job. if an additional men is hired, the job can be completed 8 days earlier. given that the number of days required to complete the job is inversely proportion to the number of men hired, find the number of additional men who must be hired in order for the job to be completed 28 days earlier.
Answer by ikleyn(52777)   (Show Source):
You can put this solution on YOUR website! .
5 men are hired to complete a certain job. If an additional  man is hired, the job can be completed 8 days earlier.
Given that the number of days required to complete the job is inversely proportion to the number of men hired,
find the number of additional men who must be hired in order for the job to be completed 28 days earlier.
~~~~~~~~~~~~~~~~~~~~~~~~~
Let "d" be the number of days for 5 men to complete the job, according to the initial plan/scenario.
We can easily find this unknown "d". Indeed, for the entire job we have this "man-day" equality
5d = 6*(d-8) ("If an additional man is hired, the job can be completed 8 days earlier.)
Which gives 5d = 6d - 48 and then d = 48.
Thus it required 48 days for 5 men to complete the job. Or, in total, the entire job is 5*48 = 240 "man-days".
Now the goal is to complete the job 28 days earlier.
In other words, the management wants to complete the job in 48-28 = 20 days.
In this case, the number of workers must be 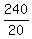 = 12.
Having this, you can easily calculate the answer.
|
|
|
