the y intercept is the value of y when x = 0.
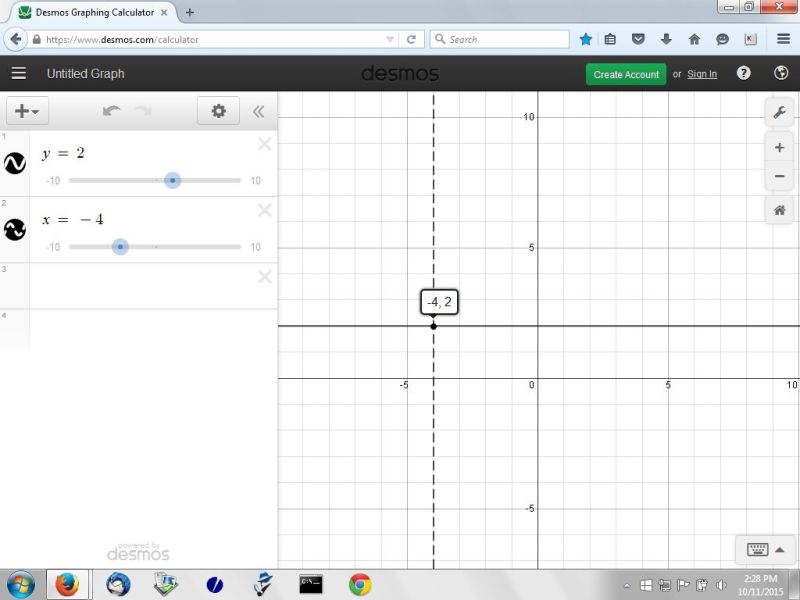
the line passes through the point (-4,2) and has no x intercept.
this means that the line never crosses the x-axis and so the value of y is never equal to 0.
in order for that to happen, the line must be parallel to the x-axis.
the equation for line A has to be y = 2.
no matter what the value of x is, the value of y will always be 2.
this means that the point (-4,2) is on the line because the coordinate point of (-4,2) means that the value of x is -4 when the value of y is 2.
here's a graph of y = 2
the line is in ax + by = c form already, with a = 0 and b = 1
you get 0x + 1y = 2 which simplifies to y = 2.
line B passes through (-3,5) and is parallel to the line x+3y=1
if it is parallel to the line x + 3y = 1, then it has to have the same slope as the line x + 3y = 1.
to find the slope, convert the formula to y = mx + b form, where m is the slope and b is the y intercept.
start with x + 3y = 1.
subtract x from both sides of the equation to get 3y = -x + 1.
divide both sides of the equation by 3 to get y = -(1/3)x + 1/3.
the slope is -1/3 and the y intercept is 1/3.
the line that passes through the point (-3,5) must have the same slope.
start with y = mx + b
replace m with -(1/3) to get y = -(1/3)x + b
since the point (-3,5) is on the line, you can replace y with 5 and x with -3 to get 5 = -(1/3)(-3) + b
now you have to solve for b to find the y intercept.
simplify to get 5 = 1 + b because -1/3 * -3 is equal to 1.
subtract 1 from both sides of the equation to get 4 = b
your equation is y = -(1/3)x + 4.
now you need to convert this to ax + by = c form.
start with y = -(1/3)x + 4
add (1/3) * x to both sides of the equation to get (1/3)x + y = 4
now you need to get rid of the fractions.
multiply both sides of the equation by 3 to get x + 3y = 12
the coefficient of the x term has to be positive, which it is, so you're done.
here's a graph of your original equation of x + 3y = 1 and the graph of your equation that goes through the point (-3,5) that is parallel to it, which is x + 3y = 12.
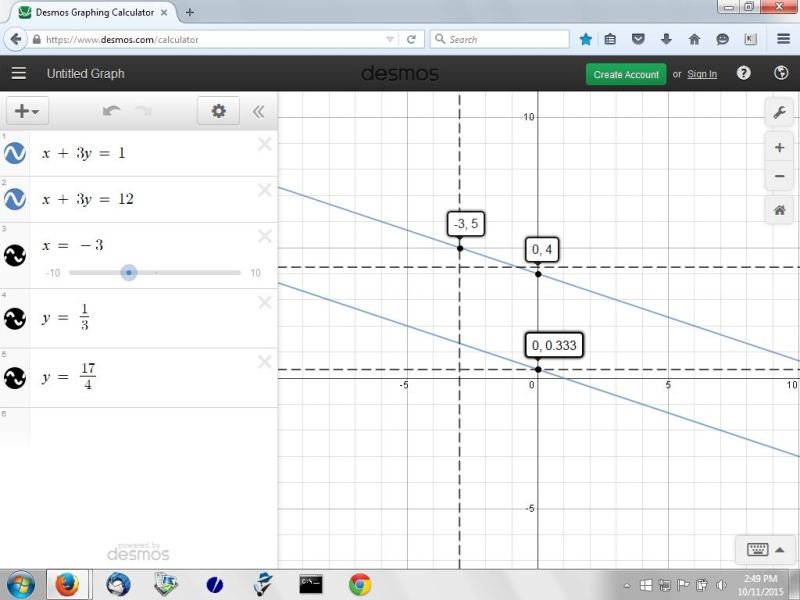
the y intercept of both lines is shown, as is the point (-3,5).
y = 1/3 when x = 0 for the original equation.
y = 4 when x = 0 for the equation that passes through the point (-3,5).
1/3 is the same as .333..... rounded to 3 decimal places.