SOLUTION: Write all of the possible whole number dimensions of a rectangle with an area of 72u^2. Any help would be greatly appreciated.

Algebra ->  Test -> SOLUTION: Write all of the possible whole number dimensions of a rectangle with an area of 72u^2. Any help would be greatly appreciated.      Log On


   

Question 714925: Write all of the possible whole number dimensions of a rectangle with an area of 72u^2. Any help would be greatly appreciated.
Answer by KMST(5328) About Me  (Show Source):
You can put this solution on YOUR website!
I assume that u is not a variable, and that u%5E2 means squared units of length.
The length of the sides of the rectangle have to be two whole numbers (positive integers) that multiplied give you 72.

We are looking for factors of 72 , meaning numbers that divide 72 evenly.

1 is an option. 72%2F1=72 <--> 1%2A72=72
The rectangle could be 1 unit wide and 72 units long.

2 works too. 72%2F2=36 <--> 2%2A36=72
The rectangle could be 2 units wide and 36 units long.

We continue with 3 and 4:
72%2F3=24 <--> 3%2A24=72 (3 units wide and 24 units long).
72%2F4=18 <--> 4%2A18=72 (4 units wide and 18 units long).

5 does not divide 72 evenly, and 7 does not work either, but 6 and 8 do:
72%2F6=12 <--> 6%2A12=72 (6 units wide and 12 units long).
72%2F8=9 <--> 8%2A9=72 (8 units wide and 9 units long).

The next whole number is 9, but we already worked through that.
8%2A9=72 and the rectangle would be the same 8 units wide and 9 units long rectangle found above. (Once you get to a factor whose square is larger than the rectangle, as in 9%5E2=81%3E72 you are finding the long side rather than the width of the rectangle).
We are done looking for factors, and we found 6 possible sets of dimensions for the rectangle:
1 unit wide and 72 units long,
2 units wide and 36 units long,
3 units wide and 24 units long,
4 units wide and 18 units long,
6 units wide and 12 units long, and
8 units wide and 9 units long.

ALTERNATE WAY:
(Ignore this part if you were not taught about this stuff and do not want to risk getting confused. It is not the easier way to the solution in this case).
The prime factorization of 72 is
72=2%5E3%2A3%5E2
We can find all factors as products of the form 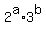2%5Ea%2A3%5Eb
with 0%3C=a%3C=3 and 0%3C=b%3C=2.
That means there are 4%2A3=12 factors (4 xhoices for a and 3 for b).
The 12 factors will come in pairs that multiply to yield 72 ,
so there will be 12%2F2=6 pairs that will be options for the shape/dimensions of the rectangle.
We can even calculate some factors.
2%5E0%2A3%5E0=1%2A1=1
2%5E1%2A3%5E0=2%2A1=2
2%5E2%2A3%5E0=2%2A1=4
2%5E3%2A3%5E0=8%2A1=8
2%5E0%2A3%5E1=1%2A3=3
2%5E0%2A3%5E2=1%2A9=9
2%5E1%2A3%5E1=2%2A3=6 and so on.
I would only use this method for large numbers with hard to find factors.