SOLUTION: Please help me verify Rolle's theorem for f(x)=(x-1)(x-2)(x-3) in the interval [1,3]

We need to find a value of x in the interval [1,3]
such that f'(x) = 0.  So we need to find f'(x)

f(x)= (x-1)(x-2)(x-3)

First we'll multiply out the right sides:

f(x)= (x²-3x+2)(x-3)

f(x)= x³-3x²-3x²+9x+2x-6

f(x)= x³-6x²+11x-6

Now we'll take the derivative:

f'(x) = 3x²-12x+11

Now we set the right side equal to zero in 
hopes of getting a value of x in the interval [1,3]

3x²-12x+11 = 0

x =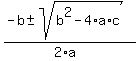 

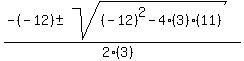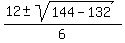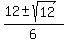x =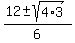 

x = 

x =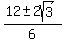 

x = 

x = 

x = 

x =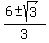  

Using the +,
x =  ≐ 2.57735 wjich is in the interval [1,3] 

Using the -,
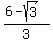x =  ≐ 1.42265 whis is also in the interval [1,3]

So there are two values of x in the interval [1,3] where f'(x) = 0.

[There only needs to be one such value to satisfy Rolle's theorem,
but it is just fine if there are more than one.]

Edwin