Question 571805: List all divisors of the following whole numbers.
A) 64
B) 24
c) 45
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! There are two strategies to find all divisors. Depending on the numbers and on your taste, you may decide on 1 or the other strategy.
STRATEGY # 1 - JUST LIST THEM
You could start with 1, and add to the list each divisor you find, while at the same time adding the quotient on the other end.
For example 2 divides 24 and the quotient is 12, so 24 is 2 times 12, and both of those numbers (2 and 12) are divisors of 24.
Here's how it would go:
DIVISORS of 64
64 divides by 1 (all numbers do), and the quotient is 64, which also divides 64, so I add both divisors to the ends of my list and have
1, ............, 64
2 also divides 64, and the quotient is 32, so I add both (2 and 32) to my list
1, 2, ........., 32, 64
3 does not divide 64, but 4 does, and the quotient is 16, so I add 4 and 16
1, 2, 4, ....., 16, 32, 64
Neither 5, nor 6, nor 7 divide 64, but 8 does, and the quotient is 8. I add 8 to the list only once, and I realize that I got to the middle of the list, and there are no more divisors.
1, 2, 4, 8, 16, 32, 64 is the whole list of divisors of 64.
DIVISORS of 24
I start with 1, ...., 24
I continue by adding 2 and 12, to get 1, 2, ...., 12, 24.
I find that 3 works too, and gives 8 for a quotient, so I add 3 and 8 to get
1, 2, 3, ....., 8, 12, 24
4 is also a divisor, and the quotient is 6, so I add 4, and 6 to get
1, 2, 3, 4, ..., 6, 8, 12, 24
5 is not a divisor, and 6 would be next, but it has already been added, and it's in the second half of the list, so there are no more divisors
1, 2, 3, 4, 6, 8, 12, 24 is the whole list of divisors of 24.
DIVISORS OF 45
1, ......, 45
2 is not a divisor, but 3 is and 45 divided by 3 is 15, so I add 3 and 15
1, 3, ...., 15, 45
4 is not a divisor, but 5 is, and 45 divided by 5 is 9, so I add 5 and 9
1, 3, 5, ...., 9, 15, 45
Neither 6, nor 7, nor 8 are divisors, and 9 was part of the last half of the list, so I am done. The divisors of 45 are only
1, 3, 5, 9, 15, and 45.
THE FACTORING AND COMBINATORICS STRATEGY
Doesn't it sound fancy? For some numbers it may work better. In this case, it seems like overkill, but I'll demonstrate.
First you find the prime factorization of the number. Then you figure out how you can combine those factors to make divisors.
For 64:
 There is only one prime factor, so our divisors would be There is only one prime factor, so our divisors would be  , ,  , ,  and so on up to and so on up to 
Because the exponent of 2 in the prime factorization was 6, we know that we had 7 choices for exponents in the divisors.
For 24:
 The divisors could have exponents 0 through 3 on the 2, and 0 or 1 on the 3. There are 4 times 2 choices, so there should be 8 divisors. With The divisors could have exponents 0 through 3 on the 2, and 0 or 1 on the 3. There are 4 times 2 choices, so there should be 8 divisors. With  , we have 1, 2, 4, and 8 With , we have 1, 2, 4, and 8 With  we get 3, 6, 12, and 24. we get 3, 6, 12, and 24.
For 45:
 Two prime factors with exponents 2 and 1, so (2+1) times (1+1) choices, meaning just 6 factors. With Two prime factors with exponents 2 and 1, so (2+1) times (1+1) choices, meaning just 6 factors. With  , we have 1, 3, and 9. With , we have 1, 3, and 9. With 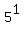 , we have 5, 15, and 45. , we have 5, 15, and 45.
|
|
|