Question 495207: Find a formula for the general term of the sequence by looking at the first five terms of the sequence.
1) (1/2, 1/4, 1/8, 1/16,.....)
2) (2,7,12,17,22,........)
3) (0,2,0,2,.....)
4) (1/2, 1/4, 1/6, 1/8, 1/10,......)
Answer by bucky(2189)   (Show Source):
You can put this solution on YOUR website! Here are the general formulas in which N is the number of the term you are looking for:
.
1) 
.
2) 
.
3) zero for N odd and 2 for N even
.
4) 
.
Try each one of these out to ensure that they work for the first 4 or five terms that you are given for each series.
.
Two types of progressions or sequences are arithmetic and geometric. Both of these progressions require you to try to try to find some common relationship that allows you to move from one term to the next term.
.
An arithmetic progression is a sequence in which each term after the first term is obtained by ADDING the same fixed number called the common difference to the preceding term. Problem number 2 is an example of this type of a sequence. Note that by carefully examining the relationship between each term and the term that follows it, there is a common difference of +5. To get from one term to the next just ADD 5. The formula that always applies to any arithmetic series is that each term is given by the relationship:
.
a + d*(n - 1)
.
in which "a" is the first term in the sequence, n is the number of the term of interest, and d is the common difference between terms.
.
So for problem 2, a = 2 (the first term), n is the number of the term you wish to know, and d = +5. Substitute these values and you have the answer for Problem 2 is:
.
2 + 5*(n - 1)
.
On the other hand, a geometric progression is a sequence in which each term after the first term in the sequence is obtained by MULTIPLYING the same fixed number called the common ratio by the preceding term.
.
Look at the terms of problem 1. Carefully examining the relationship between two successive terms will show you that to get from one term to the next you multiply the first term by  . The general formula for geometric progressions is:
.
.
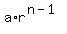
in which "a" is the first term (in this problem  , r is the common ratio (for this problem  and n is the number of the term you are interested in:
.
Substituting these values from the first problem you get:
.
.
Because the first term and the common ratio are the same for this problem, it can be simplified as follows:
.
.
In multiplying the exponent terms, because they have the common base of you can just add the exponents to get:
.
.
which, because the 1 and the -1 cancel each other, simplifies to:
.
.
and since the numerator 1 when raised to any exponent remains just 1, this further simplifies to:
.
.
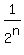
By comparing one term to the next term in Problem 4, you will notice that the denominators of the fractions are increasing ARITHMETICALLY while the numerator always stays 1.
.
So we can use the formula for arithmetic progressions on the denominator as follows:
.
.
in which for Problem 4, the first term "a" is 2, and the common difference d is also 2. Substitute these values and the formula for a term becomes:
.
.
Do the distributed multiplication in the denominator to get:
.
.
In the denominator the 2 and the -2 cancel each other and you have just:
.
.
Problem 3 has neither a common difference (sometimes +2 and sometimes -2 depending on the numbers of the term of interest) nor a common ratio. Therefore, the formulas for arithmetic or geometric progressions do not really apply. Since the terms alternate in a repeating pattern it is appropriate to find a pattern just on the basis of the number of the term "n" as shown by the answer.
.
Hope this helps you understand it better this time.
|
|
|
