SOLUTION: A random sample of n = 900 observations from a binomial population produced x = 691 successes. Give the best point estimate for the binomial proportion p. (Round your answer to th

Question 1206942: A random sample of n = 900 observations from a binomial population produced x = 691 successes.
Give the best point estimate for the binomial proportion p. (Round your answer to three decimal places.)
p̂ =
Calculate the 95% margin of error. (Round your answer to three decimal places.)
You may need to use the appropriate appendix table to answer this question.
Answer by Theo(13342) (Show Source): You can put this solution on YOUR website!
this is what i get from what i know.

p = 691/900 = probability of success = population mean proportion.
q = 209/900 = probability of failure.
s = sqrt*(p*q)/900) = .014075 = standard error.

critical z-score at 95% two-tail confidence interval = plus or minus 1.96.

the critical raw score (value of x in the formula) on the high side of the two tail confidence interval is found by the formula of z = (x-m)/s which becomes 1.96 = (x-691/900)/.014075.
solve for x to get x = 1.96 * .014075 + 691/900 = .7953647777.

the critical raw score (value of x in the formula) on the low side of the two tail confidence interval is found by the formula of z = (x-m)/s which becomes -1.96 = (x-691/900)/.014075.
solve for x to get x = -1.96 * .014075 + 691/900 = .7401907778.

round to 3 decimal places and your 95% confidence interval is from .740 to .795.

here's what it looks like on a z-score graphing calculator.

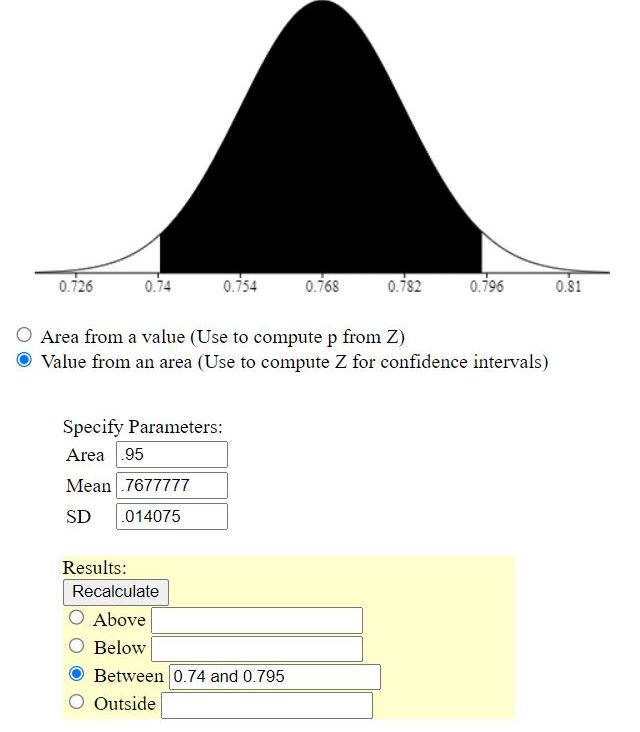
691/900 is equal to .76777..... which is the mean.
.014075 is equal to sqrt(691/900 * 209/900) / 900) which is the standard errror.

the margin of error was calculated to be (x-m) from the high side of the confidence interval which was .7953647777 minus .7677777778 = .0275869999.

the margin of error from the low side of the confidence interval is the same.

RELATED QUESTIONS
in a random sample of 900 observations from a binomial population produced x = 378... (answered by stanbon)

A random sample of n = 1200 observations from a binomial population produced x = 689. (answered by stanbon)

In a random sample of 200 observations, we found the proportion of successes to be 48%... (answered by Boreal)

A sample of 900 observations taken from a population produced a sample proportion of... (answered by stanbon)

In a random sample of 200 observations,we found the proportion of successes to be 48%.... (answered by Boreal)

Dear Tutor please help me with stats question In a random sample of 200... (answered by Theo)

Consider H0: μ=72 versus H1: μ>72. A random sample of 16 observations taken... (answered by Boreal)

In a random sample of 200 observations, we found the proportion of successes to be 48 %. (answered by Boreal)

A random sample of n=100 observations is selected from a population with u=30 and... (answered by Boreal)