Question 631073: Letting log2=a, log3=b and log5=c, how do i express:
1. log2/3 in terms of a, b, and c
2. log5/3 in terms of a, b and c
3. log8/3........... in terms of A B and C?
Answer by jsmallt9(3758)   (Show Source): (Show Source):
You can put this solution on YOUR website! You've been given the logs of 2, 3 and 5. You are also allowed to use well-known logs. With the base of "log" being 10, the log of any power of 10 (10, 100, 1000, 1/10, 1/100, etc.) are well-known and cn be used in these problems.
The keys to solving these problems is to rewrite the log in terms of the given and/or well-known logs. In this case we want to rewrite the logs in terms of log(2), log(3), log(5) and/or the log of any power of 10.
1. log(2/3)
We can see the 2 and the 3, There is a property of logs,  , which allows us to apart the log of a quotient like this: , which allows us to apart the log of a quotient like this:
log(2/3) = log(2) - log(3)
Now that we have an expression in terms of log(2) and log(3), we can express this in terms a and b:
log(2/3) = log(2) - log(3) = a - b
2. log(5/3)
Again we can see the 5 and the 3, And it is a quotient again. So this problem is a lot like number 1:
log(5/3) = log(5) - log(3) = c - b
3. log(8/3)
We can see a 3. But a 2, 5 or power of 10 is not immediately obvious. To solve this problem we have to "look inside" the 8 trying to find 2's, 3's or powers of 10. With a little effort you should be able to see that  So we start by expressing the 8 in terms of 2: So we start by expressing the 8 in terms of 2:
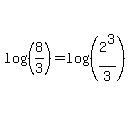
Now we can use the quotient property to split this in two:
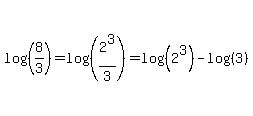
For the first log we can use another property of logarithms,  , to move the coefficient of the argument out in front: , to move the coefficient of the argument out in front:
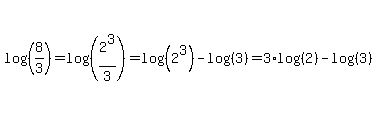
Now that we have an expression of log(2) and log(3) terms, we can substitute in the a and b:
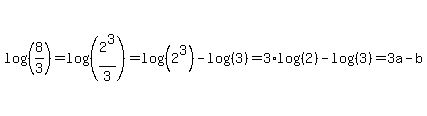
P.S. As it turned out, we never did need to use any of the well-known logs (i.e. logs of powers of 10). Just remember that in other problems we might need to use one or more of them. For example,
log(200/3) = log(200) - log(3) = log(100*2) - log(3) = log(100) + log(2) - log(3) = 2 + a - b
|
|
|