SOLUTION: log (2x+5)+log (x+1)=1
Algebra.Com
Question 326418: log (2x+5)+log (x+1)=1
Found 2 solutions by Fombitz, solver91311:
Answer by Fombitz(32388) (Show Source): You can put this solution on YOUR website!
Use the FOIL method,
Use the quadratic formula,
Use only the positive result since log function requires positive arguments.
Answer by solver91311(24713) (Show Source): You can put this solution on YOUR website!
The sum of the logs is the log of the product.
 + \log_b(y) = \log_b(xy))
\ +\ \log(x\ +\ 1)\ =\ \log\left((2x\ +\ 5)(x\ +\ 1)\right)\ =\ \log(2x^2\ +\ 7x\ +\ 5))
Use the definition of the logarithm function:
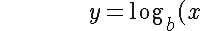 \ \ \Rightarrow\ \ b^y = x)
Hence
\ \ \ \Rightarrow\ \ 10^1\ =\ 2x^2\ +\ 7x\ +\ 5)
Solve the quadratic:
Exclude any roots that would make 
or 
outside the domain of the log function. That is to say, for either of the roots of 
the following criteria must be met: 
and 
.
John
RELATED QUESTIONS
log 4x= log... (answered by tutor_paul)
Log ( x) + Log (5 ) =... (answered by nerdybill)
{{{ log ((2x+1))=1-log((x-1))... (answered by josgarithmetic)
Log(2x+1)+log(x-1)=log9 (answered by stanbon)
log(2x-1) + log(x+2) =... (answered by stanbon)
log(2x+1)+log(x-1) (answered by Edwin McCravy)
log (2x+1) = 1-log... (answered by fractalier)
Log(3x+1)+log(1/2)+log(2x-5)=0 (answered by MathLover1)
log(2x-1) = log(x+3) +... (answered by jim_thompson5910)