Question 268070: Evaluate the logarithmic equation for three values of x that are greater than 1, three values of x that are between 0 and 1, and at x=1. State the equation of the line asymptotic to the graph (if any).
y=-base 5 logarithm x
Answer by jsmallt9(3758)   (Show Source): (Show Source):
You can put this solution on YOUR website! 
I am not going to do all this for you. But I will help with:- Finding base 5 logarithms, and
- Determining the asymptotic line
Base 5 logarithms. Normally we would pick a value for x and use the equation to find y. But there is no calculator I know of that can find base 5 logarithms. So we have to find some way to convert the base 5 logarithm into a logarithm whose base your calculator knows (base 10 or base e (ln), usually). If you know the formula for converting bases of logarithms then you can use it to rewrite your equation in a form which uses only base 10 or base e logarithms. Personally I have trouble remembering the formula. So I figure it out each time I need it. Here's how:- Rewrite the equation in exponential form.
- Find the base 10 (or base e) logarithm of each side.
- Solve this equation for y.
Let's see how this works:
1) Exponential form:

2) base 10 (or base e) logarithm of each side:

3) Solve for y. We start by using the property of logarithms,  to move the exponent out in front: to move the exponent out in front:

Divide both sides by  : :

So  which is what the conversion formula, if we remember it, says that it would be. which is what the conversion formula, if we remember it, says that it would be.
Now that we have the equation in terms of logarithms our calculator can find we are in a position to start "Evaluate the logarithmic equation for three values of x that are greater than 1, three values of x that are between 0 and 1, and at x=1."
After you find the y values for each of the specified x values you have a bunch of ordered pairs to plot on a graph.
For the asymptotic line, you need to find the domain of the equation. Logarithms must have positive arguments. So the domain of this equation is the solution to:
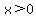 . Then, if you replace the inequality symbol with an equals sign you get the asymptotic line. So your asymptotic line is x = 0 (aka the y-axis). . Then, if you replace the inequality symbol with an equals sign you get the asymptotic line. So your asymptotic line is x = 0 (aka the y-axis).
Note the left side of inequality above is the argument of the logarithm, whatever it is. For an equation like

The domain is the solution to
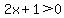
Solving this we get:

And the asymptotic line would be 
|
|
|