Question 1124860: For each of the following functions, write the formula for the function's inverse.
a. f(x)=4^x where y=f(x).
f^-1(y)= ?
b. f(x)=4(2.8)^x where y=f(x)
f^-1(y)
c. f(x)= log(x/19) where y=f(x)
f^-1(y)= ?
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! a. f(x)=4^x where y=f(x).
f^-1(y)= ?
let y = 4^x
replace x with y and y with x to get x = 4^y.
take the log of both sides of this equationt to get log(x) = log(4^y).
since log(4^y) = y * log(4), your equation becomes log(x) = y * log(4).
divide both sides of this equation by log(4) to get log(x) / log(4) = y
that's your inverse equation.
you get:
y = 4^x
y^-1 = log(x) / log(4)
if y = f(x), then y^-1 = f^-1(x) which is what you called f^-1(y).
b. f(x)=4(2.8)^x where y=f(x)
f^-1(y)
let y = 4 * 2.8^x
replace x with y and y with x to get x = 4 * 2.8^y
take the log of both sides of this equation to get log(x) = log(4 * 2.8^y)
since log(4 * 2.8^y) = log(4) + log(2.8^y) and since log(2.8^y) = y * log(2.8), this equation becomes log(x) = log(4) + y * log(2.8)
subtract log(4) from both sides of this equation to get log(x) - log(4) = y * log(2.8)
since log(x) - log(4) = log(x/4), this equation becomes log(x/4) = y * log(2.8).
divide both sides of this equation by log(2.8) to get log(x/4) / log(2.8) = y.
that's your inverse equation.
you get y = 4 * 2.8^x
y^-1 = log(x/4) / log(2.8)
if y = f(x) the y^-1 = f^-1(x) which is what you call f^-1(y).
c. f(x)= log(x/19) where y=f(x)
f^-1(y)= ?
let y = log(x/19)
replace x with y and y with x to get x = log(y/19)
log, by itself, means log10 which means log to the base of 10.
this equation can therefore be shown as x = log10(y/19).
the basic definition of logs says that x = logb(y) if and only if y = b^x.
in your problem, this translates to x = log10(y/19) if and only if y/19 = 10^x.
multiply both sides of this equation by 19 to get y = 19 * 10^x.
that's your inverse equation.
you get y = log(x/19)
y^-1 = 19 * 10^x
if y = f(x) the y^-1 = f^-1(x) which is what you call f^-1(y).
one way to determine if these equations are really inverse equations is to graph them about the line y = x.
if you then take a perpendicular to the line y = x, then the intersection of the regular equation and the inverse equation to this vertical line will be (x,y) on one side and (y,x) on the other side.
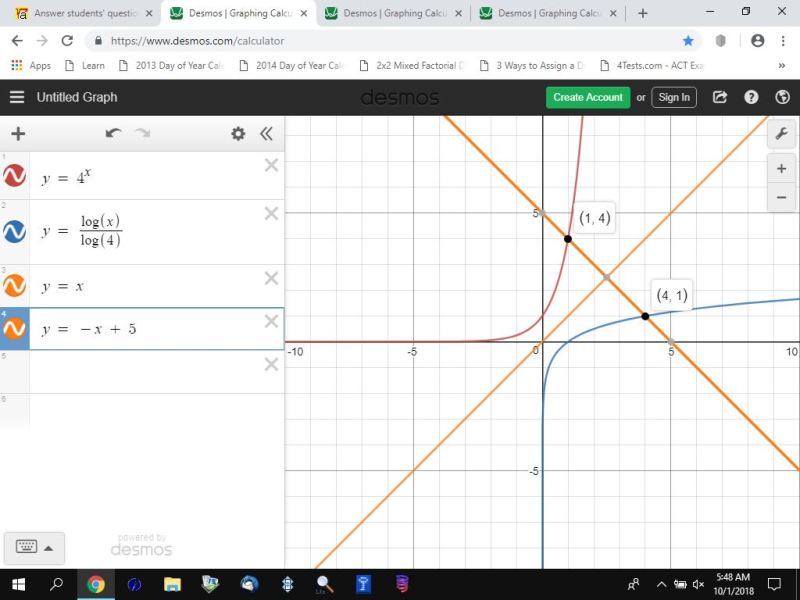
for your first problem, you have:
y = 4^x is the original equation.
y = log4(x) is the inverse equation.
the graph of that about the line y = x looks like this.
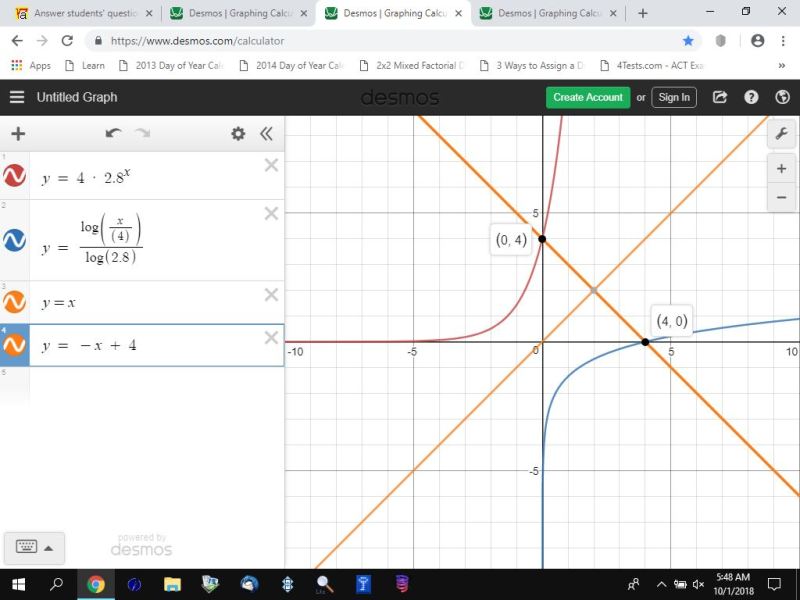
for your second problem, you have:
you get y = 4 * 2.8^x is your original equation.
y = log(x/4) / log(2.8) is your inverse equation.
the graph of that about the line y = x looks like this.
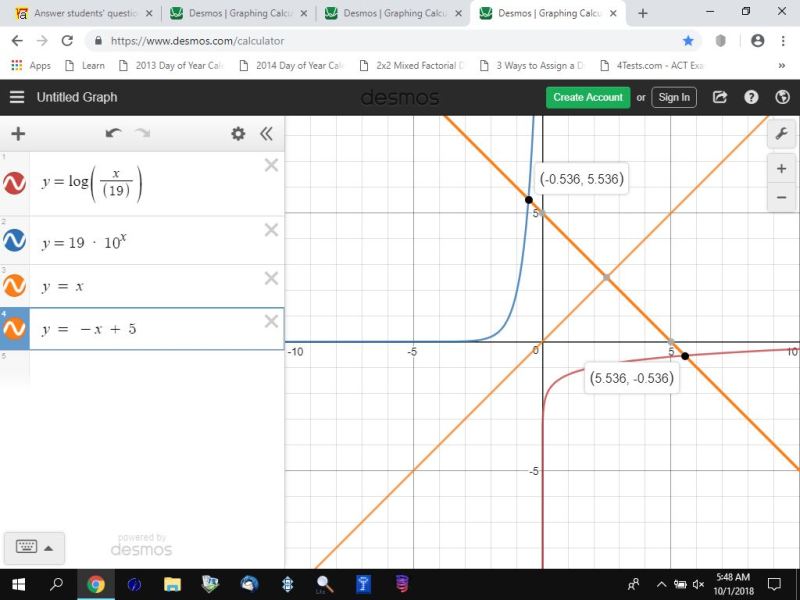
for your third problem, you have:
you get y = log(x/19) is your original equation.
y = 19 * 10^x is your inverse equation.
the graph of that about the line y = x looks like this.
here's a reference you might find useful.
https://www.purplemath.com/modules/logs2.htm
|
|
|