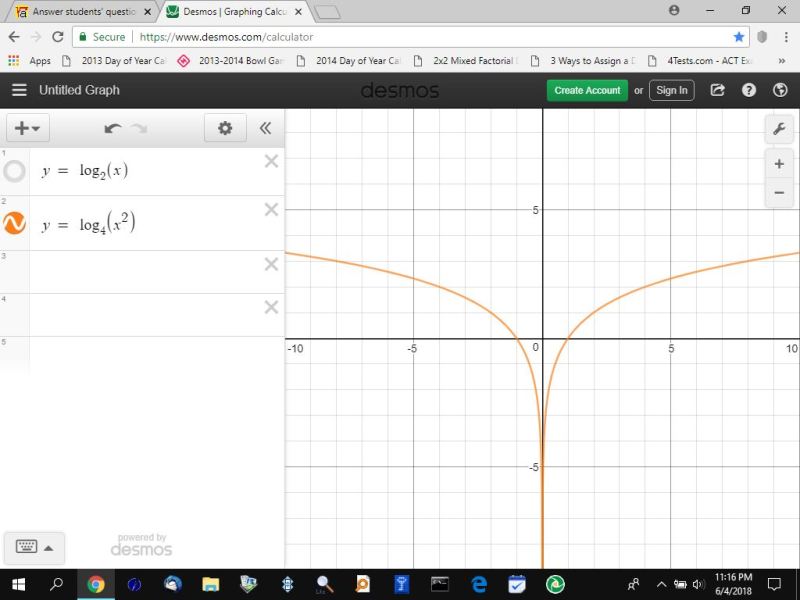
the difference is that log4(x^2) allows the value of x to be positive or negative, while log2(x) allows the value of x to be positive only.
so, if you restrict your domain to positive values of x, the 2 equations are identical.
since they are identical, then x can be any positive value.
our equation is log2(x) = log4(x^2).
it's clear that x has to be positive, since otherwise log2(x) would not provide a real answer, since x has to be > 0.
log2(x) = a if and only if x^a = x.
that's from the basic definition of of what a log is.
likewise, log4(x^2) = b if and only if 4^b = x^2.
4 is equal to 2^2, therefore 4^b is equal to (2^2)^b and you get:
(2^2)^b = x^2
(2^2)^b is equal to 2^(2b) which is equal to (2^b)^2.
you get (2^b)^2 = x^2.
take the square root of both sides of the equaiton to get:
2^b = plus or minus x.
when 2^b = plus x, the basic definition of logs states that 2^b = x if and only if b = log2(x).
that's ok, since x is positive.
however, 2^b = -x leads to log2(-x) = b which can't be, since x has to be positive.
therefore, when x is posiive, you get:
2^a = x and you get 2^b = x.
this means that a must be equal to b.
the two equations become identical as long as x is positive.
so, you get:
log2(x) = a if and only if 2^a = x.
square both sides of that equation and you get (2^a)^2 = x^2
that's the same as 2^2a = x^2 which is the same as (2^2)^a = x^2 which is the same as 4^a = x^2.
the equations are identical as long as x is positive, therefore x can be any value as long as it is positive.
i'm not sure if i explained it well, but that's what i'm seeing that the answer is.
this can be seen in the following 3 graphs.
the first graph is y = log2(x).
the second graph is y = log4(x^2).
the third graph is both equations shown on the same graph.
you can see that the black line of y = log2(x) has turned red after it was superimposed on by the orange line of y = log4(x^2).
that only happens on the right side of the graph because y = log2(x) is only valid when x is greater than 0.
y = log4(x^2) is valid for all real values of x except, i think, when x = 0.
neither graph is valid when x = 0.
here's the graphs.