SOLUTION: log1/2 16 = -4

Algebra ->  Logarithm Solvers, Trainers and Word Problems -> SOLUTION: log1/2 16 = -4      Log On


   

Question 1091577: log1/2 16 = -4
Answer by KMST(5328) About Me  (Show Source):
You can put this solution on YOUR website!
If you were not given the answer to log%281%2F2%2C16%29%22=%22%22%3F%22 , there is a way to figure out that the answer is 4 .
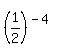If you are given that statement log%281%2F2%2C16%29%22=%22-4 , you can verify/prove that is true by showing that %281%2F2%29%5E%28-4%29%22=%2216 .

FINDING THE ANSWER:
If you need to calculate logarithms with an cumbersome base c ,
you can convert them to a more helpful base b , by using the fact that
log%28c%2Cx%29%22=%22log%28b%2Cx%29%2Flog%28b%2Cc%29 .
That is a theorem that can be formally proven,
and as a formula is useful, and easy to remember.
Applied to this case, using 2 as your helpful base
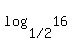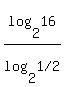log%28%221+%2F+2%22%2C16%29%22=%22log%282%2C16%29%2Flog%282%2C%221+%2F+2%22%29%22=%224%2F%28-1%29%22=%22highlight%28-4%29 .

PROVING GIVEN STATEMENT:
Here is one way to prove that 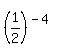%281%2F2%29%5E%28-4%29%22=%2216 :
The fraction 1%2F2 is 1 divided by 2 ,
and you know that with exponents,
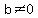%28a%2Fb%29%5En=a%5En%2Fb%5En is true, as long as b%3C%3E0 .
So, in this case,
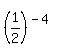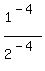%281%2F2%29%5E%28-4%29%22=%221%5E%28-4%29%2F2%5E%28-4%29%22=%221%2F2%5E%28-4%29 ,
and you know that by the definition of negative exponents
2%5E%28-4%29%22=%221%2F2%5E4%22=%221%2F16 ,
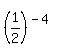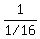so %281%2F2%29%5E%28-4%29%22=%221%2F%221+%2F+16%22%22=%2216 .
You know that
%281%2F2%29%5E4=%281%2F2%29%2A%281%2F2%29%2A%281%2F2%29%2A%281%2F2%29=1%2F16 ,
and you should know that
1%2F%221+%2F+16%22=16

If you can think of 1%2F2 only as a fraction,
you still would not that the way negative exponents are defined,
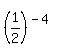
%281%2F2%29%5E%28-4%29%22=%221%2F%22%28+1+%2F+2+%29%22%5E4