Question 1141725: Given 2,5,8
Prove that none of the terms of this sequence are perfect squares
Answer by greenestamps(13203)   (Show Source): (Show Source):
You can put this solution on YOUR website!
The problem as you pose it is trivial. "This sequence" is the three numbers 2, 5, and 8. None of 2, 5, or 8 is a perfect square.
The problem you intended to pose is an interesting one, involving the infinite arithmetic sequence 2, 5, 8, ....
The numbers in this sequence are the numbers of the form 3n+2, where n is an integer. We need to show that there are no squares of integers that are of that form.
Every integer can be represented in exactly one way as either 3k-1, 3k, or 3k+1, where k is an integer.
If the integer is of the form 3k-1 or 3k+1, then the square of the integer is of the form 3n+1:
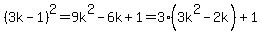

And if the integer is of the form 3k, then the square of the integer is of the form 3n:
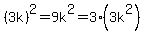
So the square of any integer is either of the form 3n or 3n+1 -- never 3n+2.
|
|
|