SOLUTION: Find the complete or particular solution on the following differential equations: y'-2y=y^2 ; y=3 when x=0 Answer: 5y=3(y+2)e^(2x)

This is a Bernoulli differential equation with n = 2, the exponent of y

let u = y1-n = y1-2 = y-1, then



We can make the first term of the original equation become u' by 
multiplying through by 







Now we also see that since y-1 = u, the above becomes







That is separable as well as a linear differential equation. I will
solve it as a linear differential equation, with P = 2 and Q = -1.
so we find the integrating factor 

 
  
Multiplying through by e2x, 



The left side is the differential of the product (e2x)(u),
so we can integrate both terms on the left together.  



On the right we take out the negative sign, insert 2 and take out 1/2:





We are told y=3 when x=0

u = y-1, substituting y=3

u = 3-1 = 













Since  u = y-1,  



Multiply through by 6





Multiply through by y






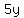Factor out 3e2x on the left



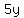Swap sides:





Edwin