group the first 2 terms and the second 2 terms as shown below:
(x^3 - 3x^2) - (4x - 12)
factor out x^2 in the first part and factor out 4 in the second part to get:
x^2 * (x - 3) - 4 * (x - 3)
factor out the (x - 3) to get:
(x - 3) * (x^2 - 4)
since x^2 - 4 is equal to (x - 2) * (x + 2), you get:
(x - 3) * (x - 2) * (x + 2)
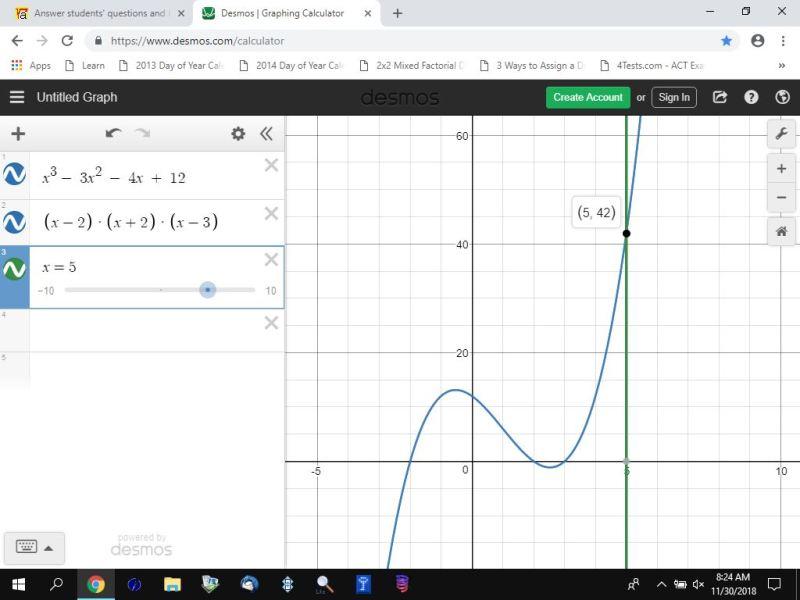
to test if this is good, take any random value of x and apply to the original form and the factored form.
i chose x = 5.
x^3 - 3x^2 - 4x + 12 = 125 - 75 - 20 + 12 = 42
(x - 3) * (x - 2) * (x + 2) = 2 * 3 * 7 = 42
you get the same value with both the original expression and the factored expression, so the factorization looks good.
i also graphed both expressions by setting them each equal to y and got the identical graph.
this is another way to see that you did it right.
my graph is shown below.