Question 570826: solve the following:
1. 6x4-11x3-35x2+34x+24
2. log(7x+2)-log(x-1)=1
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! 1. 6x4-11x3-35x2+34x+24
i graphed your first problem to see what the graph of the equation looked like.
if you're allowed to do this, it's a perfectly legitimate way of narrowing the problem down to possible solutions.
here's the graph that i created.
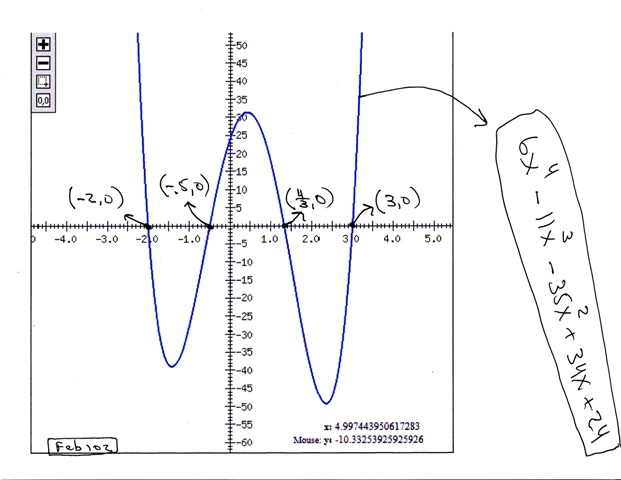
the graph shows that there are real solutions around the following points>
x = -2.0
x = -0.5
x = somewhere between 1.3 and 1.4
x = 3.0
these can be confirmed through solving of the equation by other than graphical means, or using the graphing software to find the zero points of the equation.
using the graphing software to find the zero points of the equations involves finding the intersection of the graph with the x-axis which is equivalent to the equation of y = 0.
this provides you with the value of x when the value of y = 0.
the graphing software i used indicates the zero points of the equation are at the following points on the graph.
x = -2.0
x = -0.5
x = 1.3333333 which can also be shown as x = 1 and 1/3 or x = 4/3.
x = 3.0
in this case, the graph showed the zero points fairly clearly.
in other cases, the graph will show the approximate point which can then be found exactly either through the graphing software or through algebraic calculations.
the graph itself took the grunt work out of finding where the possible real solutions were.
if we wished to find the solutions through calculations, we would do the following:
we know that -2.0 and 3.0 are roots of the equation, so we can use synthetic division to simplify the original equation.
if -2.0 and 3.0 are solutions, this means that (x+2) and (x-3) are factors.
we can reduce the equation using synthetic division by first dividing by (x+2) and then dividing the reduced equation by (x-3).
the result of that will be a quadratic equation that can then be solved using quadratic equation solving methods.
the attached diagram shows the synthetic division.

the original equation is:
6x^4 - 11x^3 - 35x^2 + 34x + 24
after dividing by (x+2), the first reduced equation becomes:
6x^3 - 23x^2 + 11x + 12
after dividing that by (x-3), the second reduced equation becomes:
6x^2 - 5x - 4
it appears that this equation won't factor easily, so we use the quadratic formula of:
x = (-b +/- sqrt(b^2-4ac))/(2a)
we set the quadratic expression equal to 0 to get:
6x^2 - 5x - 4 = 0
this puts it in standard form.
since the standard form of a quadratic equation is:
ax^2 + bx + c = 0, this means that:
a = 6
b = -5
c = -4
replacing a, b, and c in the quadratic formula with their respective values gets us:
x = (-(-5) +/- sqrt((-5)^2 - (4*(6)*(-4))) / (2*6) which simplifies to:
x = (5 +/- sqrt(25+96))/12 which simplifies further to:
x = (5 +/- sqrt(121)/12 which simplifies further to:
x = (5 +/- 11)/12
this leads to 2 solutions of x which are:
x = 16/12
x = -6/12
these solutions simplify to:
x = 4/3
x = -1/2
the decimal equivalent of these solutions is:
x = 1.333333333
x = -.5
our 4 solutions are:
x = -2.0
x = -.5
x = 1.33333333
x = 3.0
these are the same solutions as found using the graphical software.
if you have the graphing software to do it, the graphing solution is the way to go.
if you don't have graphing solutions available, you would have have to do trial and error to determine that (x+2) and (x-3) were factors and then use the quadratic formula to find the roots of the quadratic equation that was left.
it's a laborious process that is significantly simplified through the use of the graphing software.
the calculator i used was the TI-84.
it takes a little getting used to but, once you know how to use it, it works just fine.
there are others.
The TI-83 is similar but a little cheaper and still does the job adequately.
the graphical sofwtare solution won't find the complex roots of the equation.
it will only find the real roots.
if there are complex roots (a combination of real and imaginary parts), they would have to be found by other means or by graphing software that enables you to find complex roots.
i haven't seen such software nor have had occasion to use it as most problems in high school level algebra and elementary college level algebra don't require anything so sophisticated.
2. log(7x+2)-log(x-1)=1
your second equation is solved as follows:
since, in general, log(a*b) = log(a) + log(b), your first equation can be rewritten as shown below:
log((7x+2)/(x-1)) = 1
note that instead of using the general equation as log(a*b) = log(a) + log(b), we went in the reverse direction and used the general equation as log(a) + log(b) = log(a*b).
this is perfectly legitimate and is the proper way to back track from a log equation that has already been parceled out into its purest log form back to its original form.
you now have the equation:
log ((7x+2)/(x-1)) = 1
if you take the anti-log of both sides of this equation, you will get:
anti-log (log((7x+2)/(x-1)) = anti-log (1)
this can be simplified to:
(7x+2)/(x-1) = 10
the anti-log of the log of anything is anything.
in mathematical terms this would look like:
anti-log(log(a)) = a.
the anti-log of 1 is equal to 10 because the log of 10 is equal to 1.
you now have a simple equation that can be solved through normal algebraic means.
multiply both sides of that equation by (x-1) to get:
(7x + 2) = 10 * (x-1)
simplify to get:
7x + 2 = 10x - 10
subtract 7x from both sides of this equation and add 10 to both sides of this equation to get:
12 = 3x
commute this equation to get:
commute this equation means to flip each side of the equation using the general properties of algebraic equations that state if a = b then b = a. this is the law of commutation you should already know about.
the equation of 12 = 3x becomes:
3x = 12
divide both sides of this equation by 3 to get:
x = 4
the solution to this equation should be x = 4 if we did everything correctly.
to confirm, we go back to the original equation and replace x with 4 to see if the equation is true.
the original equation is:
log(7x+2)-log(x-1)=1
replace x with 4 to get:
log(7*4)+2) - log((4-1) = 1
simplify to get:
log(30) - log(3) = 1
use your calculator to get:
1 = 1
this confirms the solution of x = 4 is good.
note that when you deal with logs, the log of anything implies the base of 10 is being used, unless you specifically state what the base is.
this is what allowed us to find that the anti-log of 1 is equal to 10.
the basic property of logarithms states that:
log(b,x) = y if and only if b^y = x.
in our equation, we had log(x)) = 1 and we wanted to find the anti-log of 1 in order to find x.
by the basic property of logarithms, and using x as the variable that we are taking the log of, our equation of:
log(x) = 1 becomes:
log(10,x) = 1 because the implied base of 10 is now shown.
log(10,x) = 1 means log of x to the base of 10 equals 1.
by the basic properties of logarithms, this equation is true if and only if
10^1 = x
this simplifies to x = 10
the equation becomes:
log(10,10) = 1 which can also be shown as:
log(10) = 1 since the base of 10 is implied.
since log(10) = 1, then the anti-log of 1 is equal to 10.
|
|
|