from what you said, i will assume that a right triangle is formed.
the right triangle will be ABC
AB is the horizontal leg.
AC is the vertical leg.
BC is the hypotenuse.
the length of AC is 8.
the length of BC is 15.
the pythagorus formula is square of hypotenuse equals square of horizontal leg plus square of vertical leg.
since hypotenuse is 15 and vertical leg is 8, then the formula becomes:
15^2 = 8^2 + horizontal leg squared.
slve for horizontal leg squared to get:
square of horizontal leg = 15^2 minus 8^2 = 225 minus 64 = 161.
the length of the horizontal leg is the square root of 161 = 12.68857754.
the alternate route was the vertical leg plus the hypotenuse = 8 + 15 = 23.
the direct route was 12.68857754.
the alternate route minus the direct route = 10.31142246.
that's the additional miles that the alternate route took.
here's my diagram.
check it over and see if agrees with what your diagram looks like.
if yes, then we're good.
if no, then let me know what your diagram looks like and we can go from there.
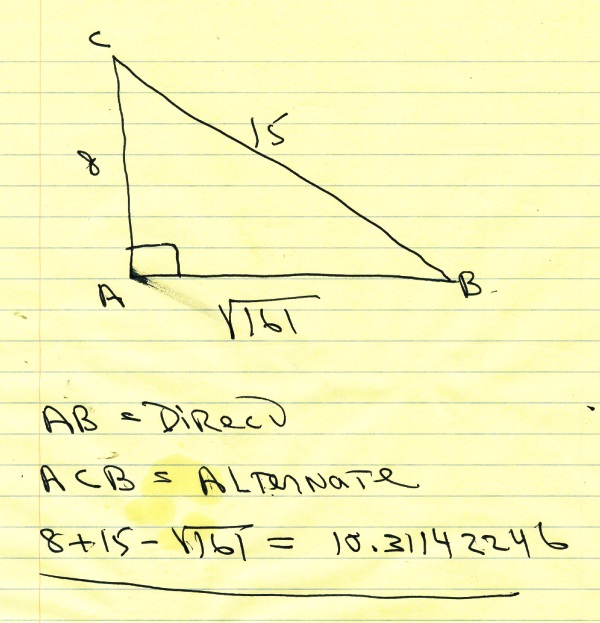
angle A is a right angle ( 90 degrees )