dog dinosaur
x y
felt 1 2 >= 300
stuffing 4 3 >= 700
trim 1 1 >= 230
cost 1.24 1.76 minimize
constraint functions are:
x + 2y >= 300
4x + 3y >= 700
x + y >= 230
x >= 0
y >= 0
objective function is:
cost = 1.74 * x + 1.76 * y
this is what you want to minimize.
using the desmos.com calculator, you would graph the opposite of the inequalities.
the feasible region is the area of the graph that is not shaded.
you would evaluate the objective function at the corner points of the feasible region.
the corner point with the lowest cost is your minimum cost solution.
the graph will look like this:
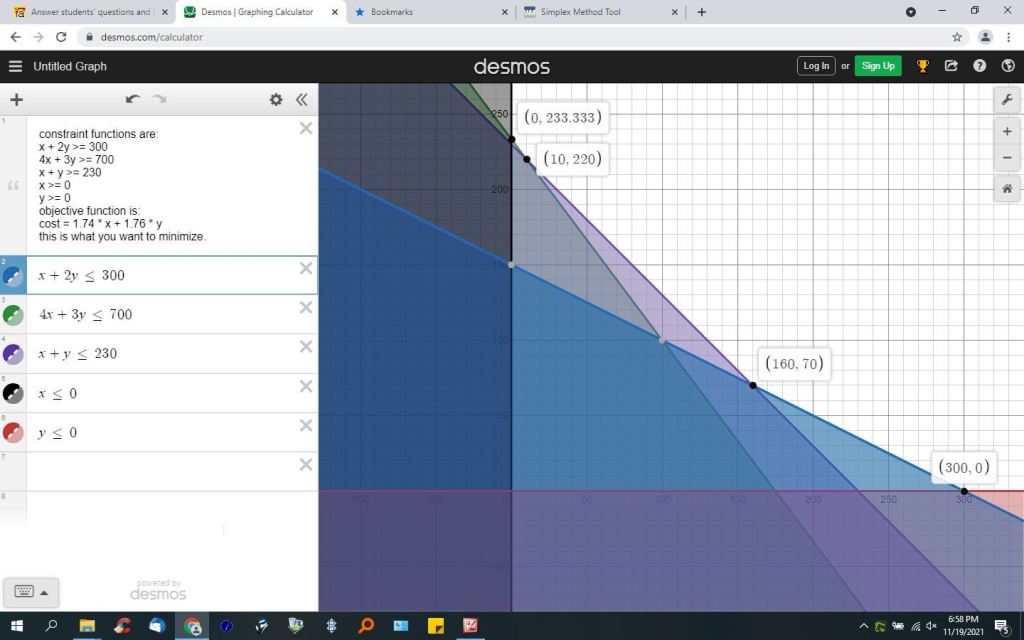
the lowest cost solution is when x = 160 and y = 70 with a cost of 321.6.
all the constraints need to be satisfied.
i checked the constraints at the minimum solution and they are all satisfied.
you were asked to provide the coefficients of the constraint inequality for felt.
the constraint inequality for felt is x + 2y >= 300
the coefficient for x is 1 and the coefficient for y is 2.