SOLUTION: Solve the rational inequality. Express answer using interval notation (show work) x^2-x-12 _________>0 x^2+x-6

Algebra.Com
Question 1164558: Solve the rational inequality. Express answer using interval notation (show work)
x^2-x-12
_________>0
x^2+x-6
Found 2 solutions by ikleyn, Theo:
Answer by ikleyn(52776)   (Show Source): You can put this solution on YOUR website!
.
Solve the rational inequality. Express answer using interval notation (show work)
x^2-x-12
_________>0
x^2+x-6
~~~~~~~~~~~~~~ 


The numerator   x^2-x-12 = (x-4)*(x+3).

The denominator x^2+x-6  = (x-2)*(x+3).


The denominator is zero at x= 3;  so this value is excluded from the domain.

The numerator   is zero at x= 4  and x=-3;  so these values are excluded from the solution set.



After canceling the common factor (x+3) in the numerator and denominator, you get the function in the form  .


It is greater than 0, when linear binomials are EITHER both negative OR both positive. 


So the solution set is the union of intervals  {x < -3} U (-3 < x < 2} U {x > 4},   or    (-oo,-3) U (-3,2) U (4,oo).      ANSWER>


See the plot below


    


    Plot y = 



Notice that the point x = -3 is the  in the domain of the function: formally, the function IS NOT DEFINED at this point.

Solved.


Answer by Theo(13342)   (Show Source): You can put this solution on YOUR website!
your inequality is:

(x^2 - x - 12)/(x^2 + x - 6) > 0

factor these quadratics to get:

(x-4)*(x+3)/((x-2)*(x+3)) > 0

the (x+3) in the numerator and the denominator cancel out and you are left with:

(x-4)/(x-2) > 0

this will be positive when x is greater than 4 or when x is smaller than 2

it till be negative when x is > 2 and < 4.

when x is greater than 4, you have a positive numerator divided by a positive denominator which results in a positive number.

when x is less than 2, you have a negative numerator divided by a negative denominator which results in a positive number.

when x is greater than 2 and less than 4, you have a negative numerator divided by a positive denominator which results in a negative number.

this can be seen in the following graph.



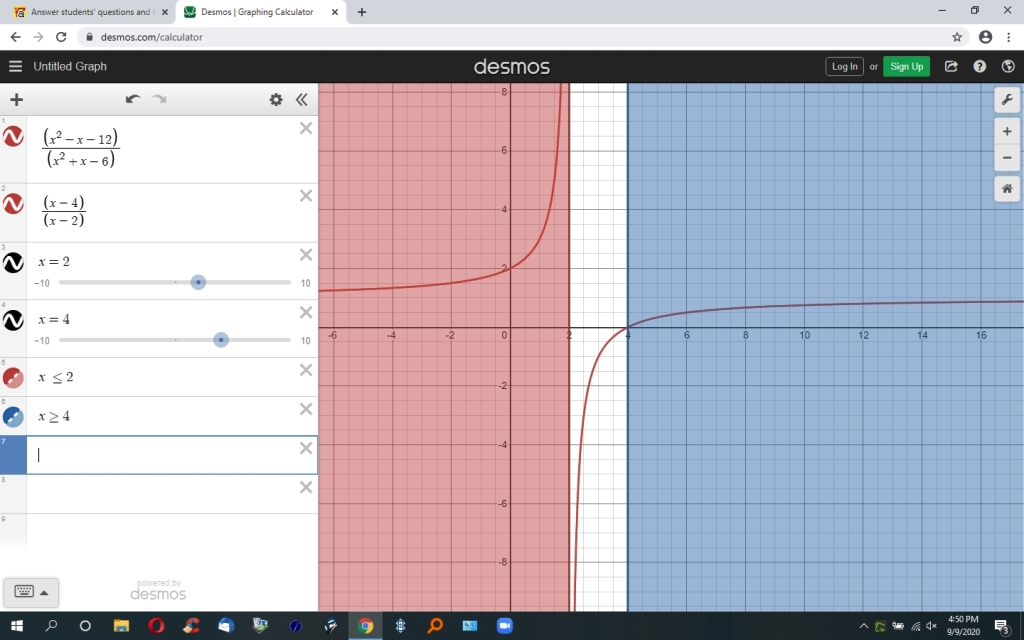
the shaded area is when the resulting number is positive.
the non-shaded area is when the resulting number if negative.


RELATED QUESTIONS

Solve the rational inequality (x-2)/(x+3) ≥ 0. Express your answer using interval (answered by josgarithmetic)
please solve the rational inequality. express answer in interval notation.... (answered by mananth)
2. Solve the inequality. Express your solution using interval notation and please show... (answered by robertb)
2. Solve the inequality. Express your solution using interval notation and please show... (answered by lwsshak3)
solve the inequality and express the solution using interval notation x^2-7x+12>0 (answered by fractalier)
Solve the following inequality. Express answer in interval notation... (answered by MathLover1)
Solve the nonlinear inequality. Express the solution using interval notation. (x + 5)(x... (answered by josgarithmetic)
Looking at the graph of y = x^2 -13 x + 30, solve the inequality x^2 -13 x + 30 > 0.... (answered by josgarithmetic,MathTherapy)
Please help me solve the following: Solve the rational inequality. Express your answer... (answered by Edwin McCravy,stanbon)