SOLUTION: Let n​,​7874185de be a​ base-ten numeral with d and e its last two digits. Give all of the choices of the​ two-digit numbers de for which n is divisible by 12.

Algebra ->  Divisibility and Prime Numbers -> SOLUTION: Let n​,​7874185de be a​ base-ten numeral with d and e its last two digits. Give all of the choices of the​ two-digit numbers de for which n is divisible by 12.      Log On


   

Question 1169153: Let n​,​7874185de be a​ base-ten numeral with d and e its last two digits. Give all of the choices of the​ two-digit numbers de for which n is divisible by 12.
Answer by Edwin McCravy(20064) About Me  (Show Source):
You can put this solution on YOUR website!
Since "de" = 10d + e,

n+=+7874185de+=+787418500+%2B+10d+%2B+e





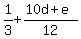n%2F12=65618208%2B1%2F3%2B%2810d%2Be%29%2F12

So 1%2F3%2B%2810d%2Be%29%2F12 must be a non-negative integer, which we can represent by the letter A

1%2F3%2B%2810d%2Be%29%2F12=A

Multiply through by 12 to clear of fractions:

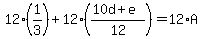
12%2A%281%2F3%29%2B12%2A%28%2810d%2Be%29%2F12%29=12%2AA

4%2B10d%2Be=12A

10d%2Be=12A-4

Since de = 10d+e must be a 2-digit number, so must 12A-4

The smallest 2-digit number is 10 and the largest 2-digit number is 99, so

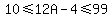10%3C=12A-4%3C=99

Add 4 to all three sides

14%3C=12A%3C=103

Divide through by 12

14%2F12%3C=12A%2F12%3C=103%2F12

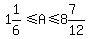1%261%2F6%3C=A%3C=8%267%2F12

Since A must be a non-negative integer,

2%3C=A%3C=8

So there are 7 choices for A, 2 through 8, inclusive

10d%2Be=12A-4

A  12A-4  de       n = 7874185de (to check) 
----------------------------------------
2   20    20           787418520 = (12)(65618210) 
3   32    32           787418532 = (12)(65618211)
4   44    44           787418544 = (12)(65618212)
5   56    56           787418556 = (12)(65618213)
6   68    68           787418568 = (12)(65618214)
7   80    80           787418580 = (12)(65618215)
8   92    92           787418592 = (12)(65618216)

The 7 choices for de are in red.  

Edwin