Question 703868: a merchant purchased a number of coats each at the same price for a total of $7200.he sold them at $400
each,thus realing a profit equal to the cost of 8 coats.calculate the number of coats purchased
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website!  =number of coats purchased =number of coats purchased
 =cost of one coat, in $ =cost of one coat, in $
The cost for  coats, in $, is coats, in $, is 
The cost for  coats, in $, is coats, in $, is 
The  coats were sold for a total of $ coats were sold for a total of $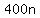
The profit realized was $ and that is equal to $ and that is equal to $ , so , so 
The system of equations to solve is

 --> -->  (dividing both sides of the equal sign by 8) (dividing both sides of the equal sign by 8)
So 
Substituting the expression  for for  in in 
we get a quadratic equation:
 --> -->  --> --> 
Dividing both sides of the equal sign by 50 we simplify that to
 which is easy to solve by factoring, which is easy to solve by factoring,
because we see that 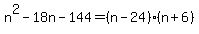
So we can write the equation as 
and realize that  and and  are solutions to the equation. are solutions to the equation.
Since the number of coats could not be negative, we discard  and our solution is and our solution is  . .
The number of coats purchased was  . .
We could even calculate the cost paid for each coat:
Substituting that value in  we find we find
 --> -->  --> -->  . .
NOTE:
If we cannot see that 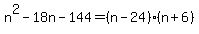 , ,
factoring is not an option to solve  . .
Then, we have to use the quadratic formula that says that the solutions to
 are given by are given by 
In the case of  we are using we are using  for for  , ,
 , ,  and and  , so , so


 --> --> 
The solutions are
 and and

|
|
|