Question 1143942: Using quadratic functions, determine the best profit the owner of a shop can have if he knows that every 5 dollar increase to his product, that costs 80 dollars, will get him 10 customers less, Everyday he sells his product to 200 customers, what is the best possible profit he could attain and prove this by using quadratic function and parabolas into the solution?
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! your equation is y = (80 + 5x) * (200 - 10x)
x is the increment of change.
y is the revenue.
when x = 0, y = 80 * 200 = 16000
what this says is, when x = 0, the price is 80 and the number of customers is 200 and the revenue is 80 * 200 = 16000.
when x is 10, y = (80 + 5x) * (200 - 10x) becomes y = (80 + 50) * (200 - 100) which becomes y = 130 * 100 = 13000.
the maximum revenue occurs when x =2.
when x = 2, y = (80 + 5x) * (200 - 10x) becomes y = 90 * 180 = 16200.
this can be seen on the graph below:
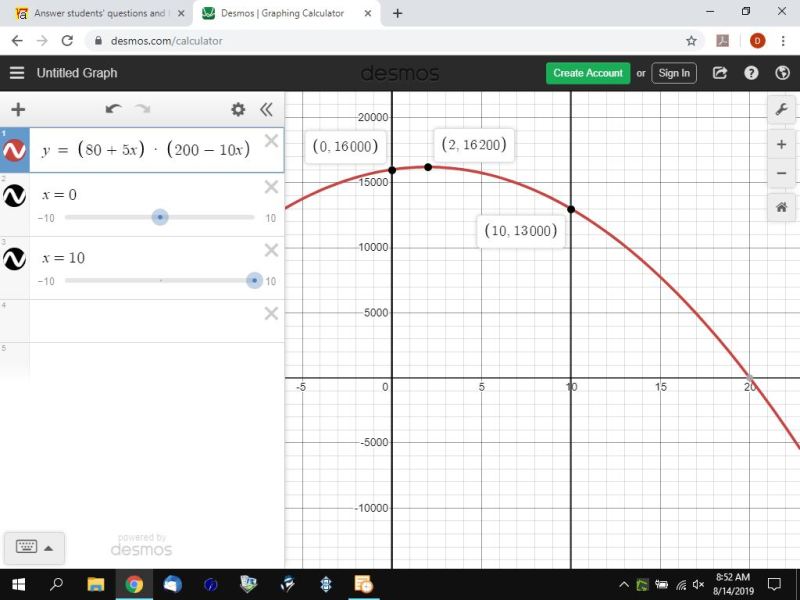
this can also be found by formula, since we have a quadratic equation.
start with y = (80 + 5x) * (200 - 10x)
simplify to get y = 16000 - 800x + 1000x - 50x^2
combine like terms to get y = 16000 + 200x - 50x^2
reorder the terms in descending order of degree to get y = -50x^2 + 200x + 16000
set y = 0 to get -50x^2 + 200x + 16000 = 0
the equation is now in standard form, where:
a = -50
b = 200
c = 16000
the maximum / minimum point of the equation is when x = -b/2a
that becomes x = -200/-100
that results in x = 2
when x = 2, the equation of y = (80 + 5x) * (200 - 10x) becomes y = (80 - 10) * (200 - 20) which becomes y = 90 * 180 which becomes y = 16200.
that's your maximum revenue, as also shown on the graph.
|
|
|