Question 885173: Find the gradient of the tangent to y(x) = x2 at A(1,1), B(-1,1) and C(2,4).
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! WITH CALCULUS:
In calculus, you are told that the slope/gradient of the tangent at a certain point
is the value of the derivative of the function at that point.
The derivative of 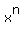 is is 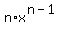 , so , so
the derivative of  is is
 . .
At point A(1,1),  so so  . .
At point A(-1,1),  so so  . .
At point A(2,4),  so so  . .
WITHOUT CALCULUS:
If you are not studying calculus,
you could write the equation of a line passing through the point given with slope  , ,
and then you would find the value of  that gives that line that gives that line
exactly one intersection point with  . .
You would do that for each point.
For point A(1,1), a point with  and and  , ,
the line would be 
Then, knowing that the tangent intersects the graph of  at only one point, at only one point,
you would know that there should be just one solution to  . .
 --> --> --> --> --> -->
has just one solution when
 --> --> --> --> --> --> --> --> . .
For point B(-1,1), a point with  and and  , ,
the line would be  . .
The equation to find the intersection point of that line and  is is
 --> --> --> --> --> --> --> --> . .
For that equation to have just one solution, it must be
 --> --> --> -->  --> --> . .
For point C(2,4), a point with  and and  , ,
the line would be  . .
The equation to find the intersection point of that line and  is is
 --> --> --> --> --> --> --> --> . .
For that equation to have just one solution, it must be
 --> --> --> -->  --> --> . .
|
|
|