Question 6611: Dear Sir/Madam,
I am confronted with the following problem:
"A box with an open top is to be constructed by cutting 3-in squares from the corners of a rectangular sheet of tin, whose length is twice its width, and then folding up the sides. What size sheet of tin will produce a box having a volume of 60 cubic inches?"
I did the following:
1) Volume = l * w * h
l = 2w
h = 3
2) 60 = 2w * w * 3
3) 6w^2 = 60
4) w^2 = 10
5) w =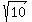 
But that is not correct. The right answer for the width is 8 inches. What did I do wrong?
Thanks in advance.
Regards,
-Mike
Answer by prince_abubu(198)   (Show Source):
You can put this solution on YOUR website! Alright. We're cool with V = l * w * h, right, and we know that h = 3 and the volume is 60 in^2. So far we've got
The trick is with the L and the W. You were right when you said that L = 2W. The length of the original sheet is twice the width of the original sheet BEFORE chopping of 3-inch by 3-inch squares on all four corners. When you chop off square corners, the actual length and width of the resulting folded box will definitely be shorter than the original L and W you started with.
Let's take the width. We decided to call it w. Now, when we cut off 3 inches from all 4 corners, that would actually chop 6 inches off the width. So the width of your box will have to be w - 6.
We know that the length = 2w BEFORE cutting off squares. Like the width, 3 inches were also chopped off the length from BOTH sides, making the actual length (of your box) 6 inches shorter. So the length of the box will be 2w - 6.
Let's now plug in the box's width and length:
 <----- We'll solve for the width eventually.
 <----- Divided both sides by 3
 <----- Performed "FOIL"
 <----- Subtract 20 from both sides.
 <---- Divide both sides by 2
 <---- "UnFOILED" or factored
Just by looking at the above equation, the width is either 8 or 1. We'll have to throw out the 1 because that measure for the width won't work if you'll have to chop 6 inches off it. The 8 would, though. If 8 is the width, and the length is twice the width, then the length is 16. So you've got a sheet that was 16" x 8".
|
|
|
