Question 632161: I cannot figure out how to solve systems by graphing. I have read and read but am so confused. I need to solve the system 2x+y=2; 6x+4y=12.
Please help me figure out the answer and show/explain how. Thanks.
Found 2 solutions by josmiceli, ewatrrr:
Answer by josmiceli(19441)   (Show Source): (Show Source):
You can put this solution on YOUR website! You have 2 straight lines. The best way to get an
idea what they look like is to convert the equations
from the standard form ( as they now are ) into
the slope-intercept form
---------------------

(1) 
and


(2) 
---------------------
(1) and (2) are now in the form 
where  = slope and = slope and  = y - intercept = y - intercept
---------------------
In (1), 
In (2), 
Both slope are negative, which means they go from
upper left to lower right on the graph, opposite to
what a positive slope does
---------------------
 gives you a point for free on each line. It gives you a point for free on each line. It
is the y-intercept point which is (0,b), or
(0, 2) for equation (1)
(0,6) for equation (2)
--------------------
Now you just need 1 other point for both lines, and
since 2 points determine a line, you can draw
each line. Where the lines intersect is the solution
to the system of lines
--------------------
To find the other point, just plug in any value for
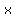 , and read off the value for , and read off the value for 
For example:
(1) 
I'll pick 
(1) 
(1) 
So, I have the point (1,0)
and
(2) 
I'll pick 
(2) 
(2) 
(2) 
So, I have the point (2,0)
---------------------
Now you have this information about the lines:
Line (1):
(0,2)
(1,0)

----------
Line (2):
(0,6)
(2,0)

----------
And that's all you need
Answer by ewatrrr(24785)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Hi,
Solve the system by putting each of their graphs on the same graph
the point they intersect at: (-2,6) is the solution for this system

If You are having difficulty graphing each of the linear equations:
find at least 2 (x,y)points for each and connect pair of the 2 points with their
respective line
2x+y=2 x = 0 ⇒ y = 2, y = 0 ⇒ x = 1 (0,2) and (1,0) on this line
6x+4y=12 x = 0 ⇒ y= 3, y = 0 ⇒ x = 2 (0,3) and (2,0) on this line

|
|
|