Question 1198712: In 2012, the population of a city was 6.97 million. The exponential growth rate was 3.87% per year.
a) Find the exponential growth function.
b) Estimate the population of the city in 2018.
c) When will the population of the city be 10 million?
d) Find the doubling time.
Answer by Shin123(626)   (Show Source): (Show Source):
You can put this solution on YOUR website! a) If the city grows at 3.87% per year, that is equivalent to multiplying by 1.0387. Therefore, the equation is  , where , where  is the population, and is the population, and  is the number of years after 2012. is the number of years after 2012.
b) 2018 is 6 years after 2012, so we would have  . Plugging this into our equation, we get . Plugging this into our equation, we get  . We can simply plug this into a calculator to get . We can simply plug this into a calculator to get  . .
c) Since  is the population, we can plug in 10 million for is the population, we can plug in 10 million for  and solve for and solve for  . .
We have the equation  . Dividing both sides by . Dividing both sides by 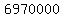 , we get , we get  . Taking the natural log of both sides, we get . Taking the natural log of both sides, we get  . Using logarithm rules to take the exponent out, we get . Using logarithm rules to take the exponent out, we get  . Dividing both sides by . Dividing both sides by 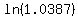 , we get , we get  . Plugging this into a calculator, we get . Plugging this into a calculator, we get  . Since . Since  is the number of years after 2012, the population will be 10 million in 2021. is the number of years after 2012, the population will be 10 million in 2021.
d) To find the doubling time, we can solve the equation  , since , since 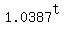 is how much the population is growing. We can take the natural log of both sides to get is how much the population is growing. We can take the natural log of both sides to get  . We can use logarithm rules to take out the exponent, which will give . We can use logarithm rules to take out the exponent, which will give  . We can divide both sides by . We can divide both sides by 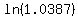 to get to get  . Finally, we can plug this into a calculator to get . Finally, we can plug this into a calculator to get  . .
|
|
|