Instead of doing your problem for you, I'll do one using different numbers which
you can use as a model to do yours by. Here's the problem I'll do:
Find the equation of the line passing through the point (−9,5) and
perpendicular to the line y=−27x−623.
First we find the slope of the line y=−27x−623 by comparing it to y = mx+b,
and we see that the slope m is -27.
The slope of a line perpendicular to a given line has a slope which is the
negative reciprocal of the slope of the given line. So we take the reciprocal
of -27, which is -1/27, and change its sign. So the slope of the perpendicular
line is 1/27. Since it passes through (-9,5), we use to point-slope form which
says the equation of the line through (x1,y1) and having
slope m is:
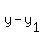

 In this case (x1,y1) = (-9,5), and m = 1/27
In this case (x1,y1) = (-9,5), and m = 1/27





 That's in point-slope form.
Now do yours the same way using your numbers.
Edwin
That's in point-slope form.
Now do yours the same way using your numbers.
Edwin