SOLUTION: A landscaping supply company produces decorative stones. A ton of coarse stones requires 2 hours ofcrushing, 5 hours of sifting, and 8 hours of drying. A

Question 1184530: A landscaping supply company produces decorative stones. A ton of coarse stones requires 2 hours ofcrushing, 5 hours of sifting, and 8 hours of drying. A ton of fine stones requires 6 hours of crushing, 3hours of sifting, and 2 hours of drying. The coarse stones sell for$400 per ton. The fine stones sell for$500per ton. In a work week, the plant is capable of 36 hours of crushing, 30 hours of sifting, and 40 hours ofdrying. Based on the demand forecast, the quantity of coarse stones produced should be at least twice thequantity of fine stones produced.
First
1. Formulate an optimization model to decide how much of each kind of stones to produce to maximizetotal revenue.
2. Solve your model using the Excel solver.
3. Using a two-dimensional plot, solve your model graphically.
Then, by modifying your two-dimensional plot, answer the following questions:
4. How much would it be worth to get another hour of crushing time?
5. How much would it be worth to get another hour of sifting time?
6. Could you find the range of the prices for the fine stones such that in the optimal solution, the quantity of coarse stones produced is exactly twice the quantity of fine stones produced.
Answer by Theo(13342) (Show Source): You can put this solution on YOUR website!
let x = the number of tons of coarse stone.
let y = the number of tons of fine stone.

your objective function is:
400 * x + 500 * y (revenue)

your constraint functions are:
2x + 6y <= 36 (crush hours)
5x + 3y <= 30 (sift hours)
8x + 2y <= 40 (dry hours)
x >= 2y (ratio of coarse stones to fine stones)
x >= 0
y >= 0

using the desmos.com calculator (https://www.desmos.com/calculator

you would graph the opposite of the constraint inequalities.
your feasible region is the area on the graph that is not shaded.
you would evaluate each corner point of the feasible region, using the objective function.

the graph looks like this:

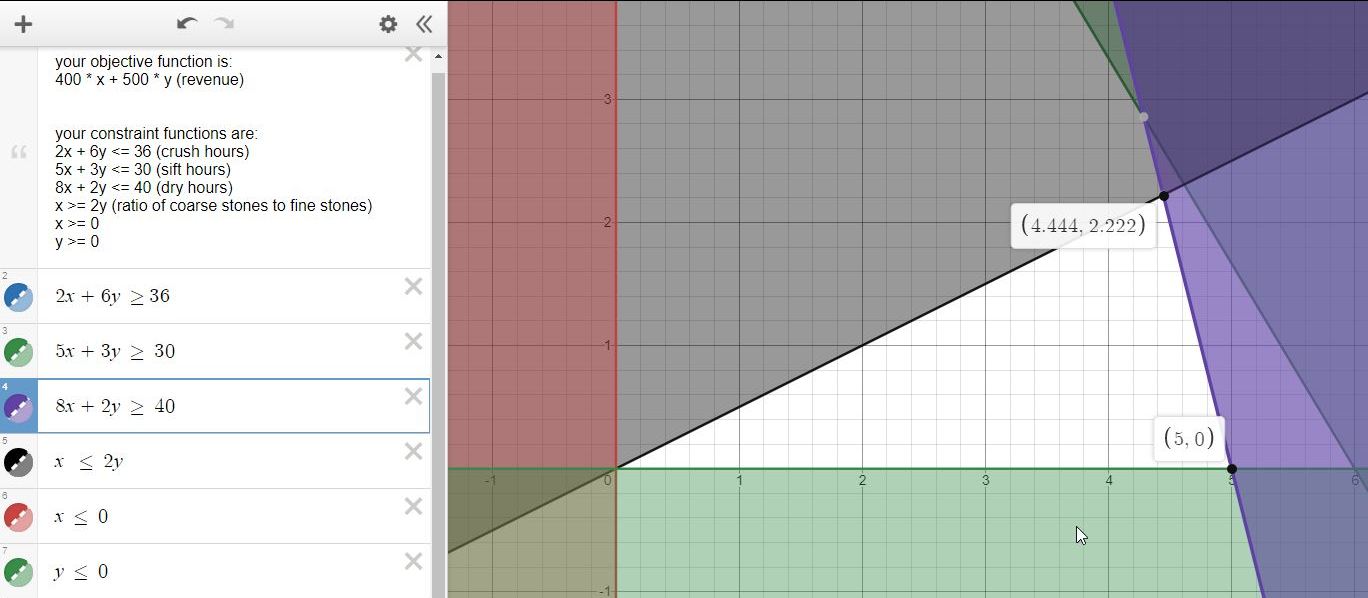
adding 1 hour to crush hour availability and adding 1 hour to sift hour availability doesn't change the result, the main reason being because of the requirement that the ratio of coarse stones to fine stone must be greater than or equal to twice the number of fine stones.

here's the graph with the added hours of availability to crushing and sifting.

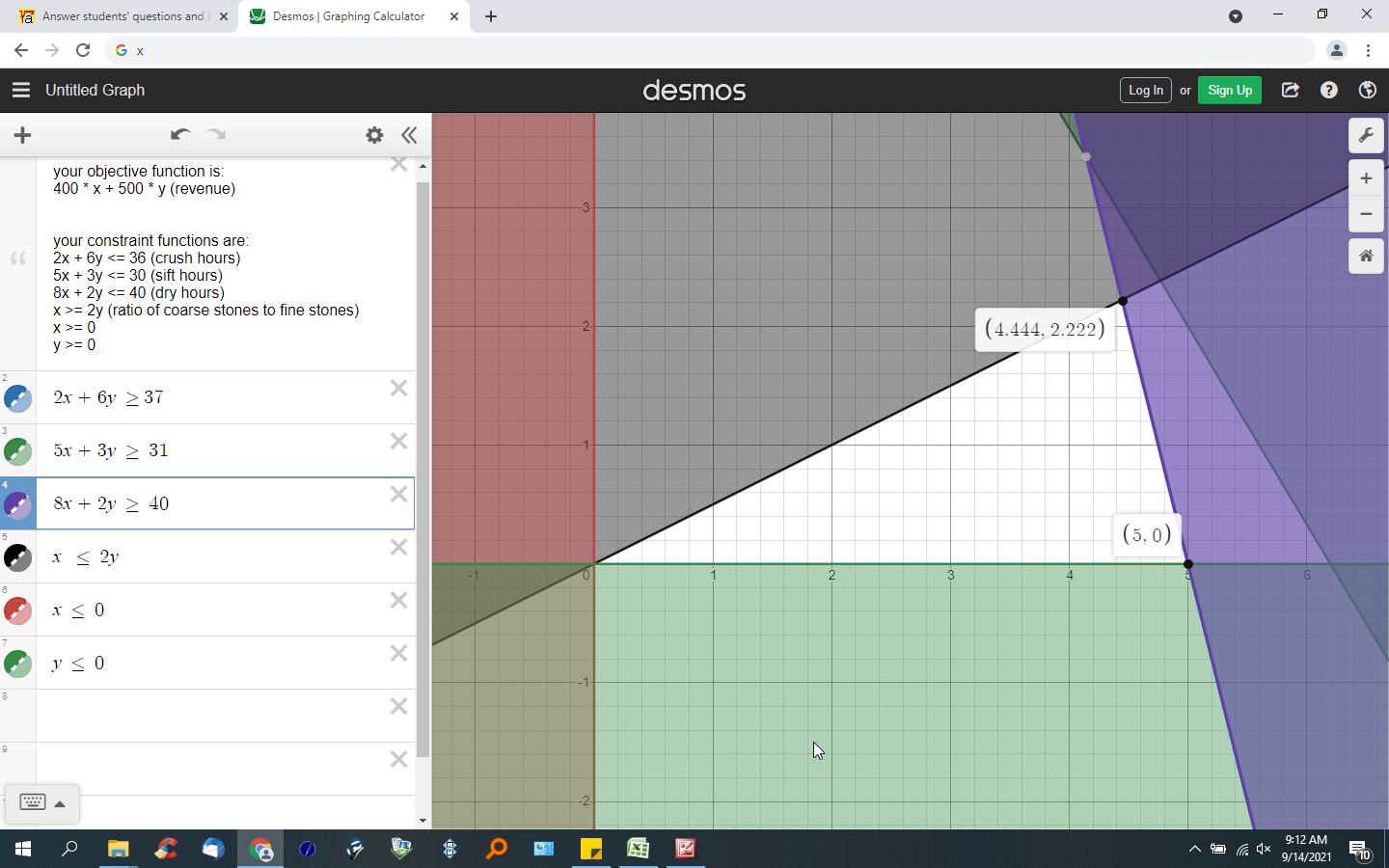
the maximum solution in both cases is 400 * 4.444 + 500 * 2.222 = 2888.6.

the next possible solution is at (5,0) where the revenue = 400 * 5 = 2000.

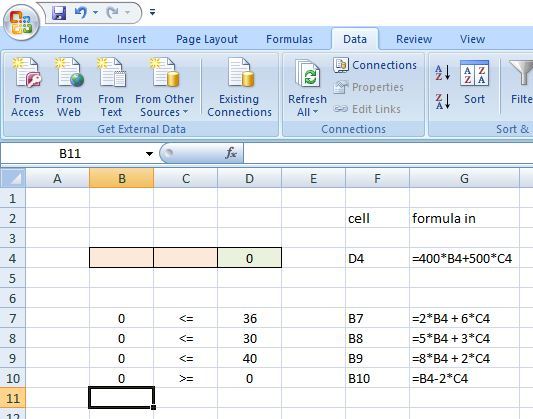
the excel solution is shown below:

before the analysis:

after the analysis:

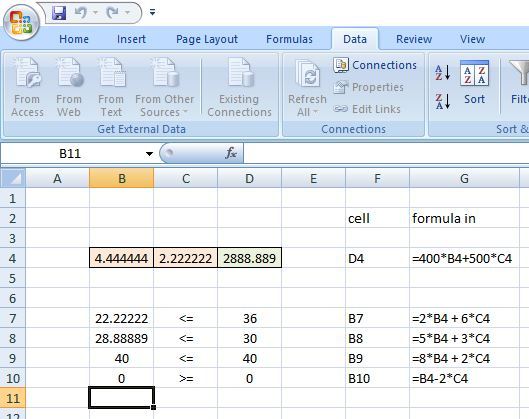
after changing the crush hour and sift hour availability.

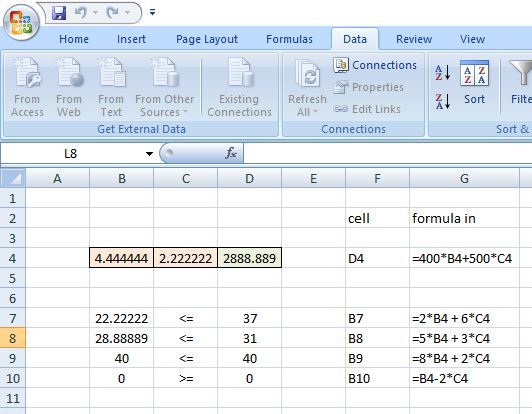
because of the constrants, the maximum revenue will either be at (4.444,2.222) or at (5,0).

the maximum revenue is at (4.444,2.222) = 2888.6.

the next possible maximum is at (5,0), where the revenue is equal to 2000.

changing the price of the fine stone will only affect the solution at (4.444,2.222).

it will have no affect at (5,0) because there are 0 tons of fine stone at that corner point.

consequently, you can only drop the price of the fine stones at (4.444,2.222) until the revenue is less than 2000 there.

my calculations show that a price of less than 100.090009 for the fine stones should change the maxim revenue solution to be at (5,0) rather than at (4.444,2.222).

the revenue at (5,0) remains the same at 1000.

the revenue at (4.444,2.222) becomes 400 * 4.444 + 100.090009 * 2.222 = 2000.

any price less than 100.090009 for the fine stones would change the maximum revenue from at (4.444,2.222) to (5,0).

for example, 400 * 4.444 + 100.09 * 2.222 = 1999.99998, making the maximum revnue at (5,0) instead because it's still 2000 there.

RELATED QUESTIONS
A landscaping supply company produces decorative stones. A ton of coarse... (answered by CPhill)

You make decorative stones for landscaping. A ton of coarse stones requires 2 hours of... (answered by Theo)

A bag contains 3 blue stones, 5 red stones, and 2 white stones. What is the probability... (answered by stanbon)

Laura is making a patio in Her backyard using paving stones. she buys 44 paving stones... (answered by farohw)

A verandah is 40m long and 15m broad . It is to be paved with stones ,each measuring 6dm... (answered by MathLover1)

1. The length of the sides of a square swimming pool are all s units long. The pool is... (answered by ankor@dixie-net.com)

Kristen is constructing a circular outdoor patio built from paving stones. The diameter... (answered by mananth,ikleyn,josgarithmetic)

Rose has 56 stones that are 6 more than one-half of my stones. How many stones do I... (answered by ikleyn)