Question 1101820: Aman started a business with an aim of making it grow and become aregional business within Uganda and even become international in the future. in the stages the business was handling basically the supply of laptops and telephones. Each laptop was supplied at aprice of ugshs2000000 where as every phone was supplied at a price of ugshs 500000. The management realised that in this business, supply of each laptop costs him ugshs 800000 whereas supply of a telephone costs him ugshs 100000. To be able to supply these products tp the customer, the businessman has to ensure that the he uses fuel for his car as well as time to move around delivering the products. To deliver a laptop, he uses 2liters of fuel and 3hours while to deliver a phone he uses 4liters of fuel and 1 hour of moving around, in aparticular month, he found that he has amaximum of 30hours and 80 liters of fuel.Establish the number of phones and laptops that should be distributed in oredr to maximise profits in the and compute the profit?
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! his revenue is 1 million per laptop and .5 million per cell phone
his cost is .8 million per laptop and .1 million per cell phone.
his profit is 1.2 million per laptop and .4 million per cell phone.
let x = the number of laptops and y = the number of cell phones sold.
profit is equal to 1.2 * x + .4 * y (in millions)
that's your objective function.
he uses 2 liters of fuel to deliver a laptop and 4 liters of fuel to deliver a cell phone.
he has a maximum of 80 liters of fuel that he can use.
2 * x + 4 * y <= 80
that's your fuel constraint function.
he uses 3 hours of travel time to deliver a laptop and 1 hour of travel time to deliver a cell phone.
he has a maximum of 30 hours of travel time that he can use.
3 * x + 1 * y <= 30
that's your travel time constraint function.
you want to graph the constraints and find the feasible region and then analyze the objective function at the corner points of the feasible region.
your constraint functions are:
2 * x + 4 * y <= 80
3 * x + 1 * y <= 80
x >= 0
y >= 0
you will graph:
2 * x + 4 * y = 80
3 * x + 1 * y = 80
x = 0
y = 0
you will then find the area on the graph that satisfies the constraints.
your graph will look like this.
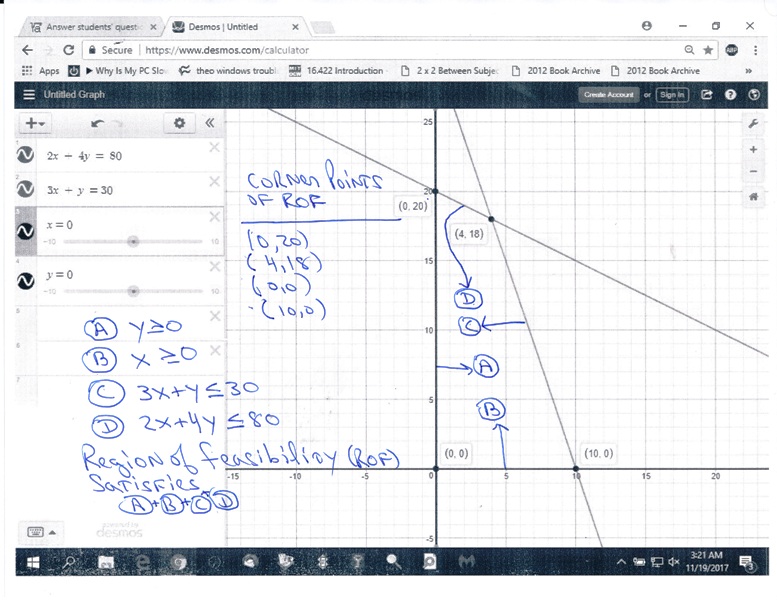
your region of feasibility is:
above the line x = 0
to the right of the line y = 0
below and to the left of the line 3x + y = 30
below and to the left of the line 2x + 4y = 80
the corner points of this feasible region are:
(0,20)
(4,18)
(10,0)
(0,0)
you examine your objective function of 1.2 * x + .4 * y at each of these corner points to find the point that has the maximum profit.
(0,20) yields a profit of 8 million.
(4,18) yields a profit of 12 million.
(10,0) yields a profit of 12 million.
(0,0) yields a profit of 0 million.
looks like you have 2 corner points that will yield the maximum profit.
those are (4,18) and (10,0)
your constraints have to be satisfied at each of these corner points.
the constraint functions are, once again:
2 * x + 4 * y <= 80 (fuel constraints)
3 * x + 1 * y <= 30 (time constraints)
x >= 0
y >= 0
at the corner point of (4,18):
fuel used is 2*4 + 4*18 = 8 + 72 = 80 liters - constraint satisfied.
time used is 3*4 + 1*18 = 12 + 18 = 30 hours - constraint satisfied.
at the corner point of (10,0):
fuel used is 2*10 + 4*0 = 20 + 0 = 20 liters - constraint satisfied with 60 liters not used.
time used is 3*10 + 1*0 = 30 + 0 = 30 hours - constraint satisfied.
x >= 0 and y >= 0 constraints are satisfied at all points.
the bottom line is you have a tie.
you can either sell 4 laptops and 18 cell phones or you can sell 10 laptops and 0 cell phones and your profit will be maximized based on the objective function.
the objective function, however, doesn't tell the whole story.
there is a cost for fuel that is not being considered.
there is a cost for delivery time that is not being considered.
even without considering that cost, (10,0) gives you the same profit as (4,18) and uses the same amount of hours, but uses less fuel, so you would probably go with (10,0).
all coordinate points are in the form of (x,y).
for example, the coordinate point of (4,18) means that the value is 4 and the value of y is 18.
therefore:
given that your profit equation is as stated, and given that no costs for fuel or delivery time are considered, i would go with (10,0) because it uses up less of the constraints while delivering the same profit.
note that i put revenue and supply cost in millions.
this makes graphing easier.
laptop revenue is 2,000,000 and supply cost is 800,000 per laptop.
that's 2 million minus .8 million = profit of 1.2 million per laptop.
cell phone revenue is 500,000 and supply cost is 100,000 per cell phone.
that's .5 million minus .1 million = profit of .4 million per cell phone.
|
|
|