Question 93127: if z1=2+j, z2=3+j and z3=j3
what is the equivalent impedance z if
1/z= 1/z1 + 1/z2 + 1/z3 ?? this was a question given to us for homework and it was not in any text book
Found 2 solutions by Edwin McCravy, bucky:
Answer by Edwin McCravy(20060)   (Show Source): (Show Source):
You can put this solution on YOUR website! if z1=2+j, z2=3+j and z3=j3
what is the equivalent impedance z if
1/z= 1/z1 + 1/z2 + 1/z3 ?? this was a question given to us for homework and it was not in any text book
You didn't copy that z3=j3 right. It's gotta be something else. Fix it and
post again.
Edwin
Answer by bucky(2189)   (Show Source): (Show Source):
You can put this solution on YOUR website! You are given three impedances:
.

 and and
 <== notice that this presumes that the impedance is so inductive that the resistance of the device is negligible. <== notice that this presumes that the impedance is so inductive that the resistance of the device is negligible.
.
The real part of these impedance is resistance and the imaginary part (called the reactance
and identified as the j terms) are inductances. (You know they are inductances because the
sign of the j terms is plus. If the sign of a j term is negative, then it is a capacitance.)
.
For the first problem you are asked to find  . This is a series connection . This is a series connection
of the three impedances and  is the equivalent impedance. You could take out the is the equivalent impedance. You could take out the
three impedances in a circuit and replace them by the equivalent impedance without effect.
.
In finding  all you need to do is add the three impedances. You do this by all you need to do is add the three impedances. You do this by
adding their real parts and then adding their imaginary parts. Where I listed the three
impedances above, you can just add them in their columns. Adding down the column of real
parts you get 2 + 3 + 0 = 5. And adding down the column of imaginary parts you get
j + j + j3 = +5j. (Note j is the same as j1. So the imaginary parts are j1 + j1 + j3 and
the addition is j(1+1+3) = +j5).
.
So the answer to the first problem is the combination of these two parts, the real part
which is 5 and the imaginary or reactive part which is +j5. Therefore, we say:
.

.
You convert this to polar form just as you would in coordinate geometry. You start at
the origin of an x-y coordinate system and you go +5 units along the x-axis. (That
represents the real part of your answer.) Then from that point (+5 on the x-axis)
you go vertically up (the +j direction) +5 units which represents the imaginary or reactive
part of the answer. [On a graph you are now at the point (5,5).] Now draw a line connecting the
origin with this point (5,5). What you have now is an Argand diagram of the answer, and the
Argand diagram consists of the 5 units along the x-axis, the 5 vertical units from that
point to the point 5,5 and the line connecting the origin to the point (5,5). Just remember
that the real part of the answer (the resistance) is along the x-axis, and the imaginary part
(the vertical) represents the j component of the answer.
.
To find the polar form of the answer you need to look at the Argand diagram and find the
hypotenuse of the right triangle. The hypotenuse will be the magnitude of the answer and
the angle between the x-axis and the hypotenuse will be the polar angle you need.
.
From geometry you may recall that a right triangle that has two legs that are equal in
length is a 45-45-90 degree triangle. Therefore, you know that the angle between the
x-axis and the hypotenuse is 45 degrees. You can use the Pythagorean theorem to find
the length of the hypotenuse (or you could use trig). The Pythagorean theorem tells you to
square each of the legs and add these squares to find the square of the hypotenuse.
So for this problem we have:
.

.
and since  the problem becomes: the problem becomes:
.

.
To find h just find the square root of 50. You can do it as follows:
.

.
Now you know that the magnitude and angle (the polar form) is 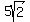 or 7.0711 or 7.0711
at an angle of 45 degrees which is often written as 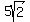 /45 or 7.0711/45 where the /45 or 7.0711/45 where the
45 is underlined and is followed by the little "o" degrees symbol. (Hard to type the exact
way it is written.)
.
Now for the second part of the problem. A little tougher because of the math manipulations,
but pretty straightforward.
.
The given formula is:
.

.
This is the formula for finding the equivalent impedance of three impedances connected in parallel.
There are several ways this could be done, but let's crank through a straightforward
method. Begin by substituting into the formula the values for the three impedances
to get:
.

.
Next recognize that the common denominator on the right side of this equation is:
.

.
Letís multiply this out combine terms. Remember in multiplying that j times j is j squared
and by definition j squared is -1.
.
First letís begin by multiplying 
.
Next multiply that answer times j3:
.
 which in more standard form becomes: which in more standard form becomes:
.

.
If we put all three terms over the common denominator, each term's numerator consists of
the product of the other two terms that were not its denominator. In other words the equation
becomes:
.

.
Now letís multiply out each of the numerators in the three terms.
.
First numerator: 
.
Second numerator: 
.
Third numerator: 
.
Now add all the numerators over the common denominator:
.

.
Now we can get the answer for  by just inverting both sides of this equation to get: by just inverting both sides of this equation to get:
.

.
Just to make things a little more conventional, letís factor -1 from both the numerator and
denominator of this answer so that the real portions of answer are positive. This factoring
results in:
.

.
This is not in a useful form yet. We can convert the denominator of this answer by multiplying
it by its conjugate. The conjugate has the same real part and imaginary part, but the imaginary
part has the opposite sign. In this case the denominator is  so its conjugate is so its conjugate is
 . When we multiply the denominator by . When we multiply the denominator by  , we must also multiply , we must also multiply
the numerator by  . So we get: . So we get:
.

.
Multiplying the denominator by its conjugate results in:
.

.
Then multiplying the numerator by the conjugate of the denominator:
.

.
This further multiplies out to:
.

.
Subtracting the two j terms shortens this to:
.

.
The last term involves minus a minus term which is positive:
.

.
The two real parts add and the numerator becomes:
.

.
This gets put over the real denominator which we found to be 401:
.

.
Dividing the two terms by 401 results in:
.

.
The Argand diagram will start at the origin and go to the right on the x-axis 0.7855 units.
From that point it will go vertically upward 0.7107 units. You are now at the point
(0.7855, 0.7107). Draw a line from the origin to that point. Again, as in the first
problem, this is the Argand diagram for the equivalent impedance.
.
Next we will use the Argand diagram to find the polar form. The polar form requires that
you have a magnitude and an angle. The magnitude is the length of the hypotenuse in the
Argand diagram, and you can use either the Pythagorean theorem or trig functions to get
the magnitude. This time letís use trig. We know that the tangent is defined by the side
opposite divided by the adjacent side of the angle. In this problem the side opposite the
angle we are looking for is the vertical side and its length is 0.7107. The adjacent side
is the horizontal side of the triangle and its length is 0.7855. So the tangent of the angle
we are looking for is:
.

.
That means that the angle has a tangent of 0.9048. Using the the tan^(-1) function key
on a calculator we find that the angle with a tangent of 0.9048 is 42.1388 degrees. So
we have half of what we need for the polar form. We still need the hypotenuse and
we can get that using either the sine or cosine function. Letís use the sine. The
definition of the sine is:
.

.
If we multiply both sides of this equation by the hypotenuse we get:
.

.
Then divide both sides by  to get: to get:
.

.
Now we can plug in values. We know the side opposite is 0.7107 and 
is the sine of 42.1388 degrees. From a calculator this is 0.6709. So our equation
with these values is:
.

.
So the polar form of this impedance is 1.0593/42.1388 which is read as 1.0593 ohms at 42.1388
degrees.
.
Lots of work. Hope this all makes sense to you and you can figure out from this the basics of
finding equivalent impedances for series and parallel circuits.
|
|
|