SOLUTION: The question must be answered in trigonometric form: 4i / (-1+ sqrt(3)i) Thank you!

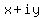
First get it in the form x+iy by multiplying numerator
and denominator by the conjugate of the denominator: 





Change both i²'s to (-1):





Factor 4 out of the numerator:









So the rectangular form is: 



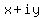
That is represented by the vector (line) connecting the origin to the point 
(x,y)= (,-1), We draw a perpendicular to the x-axis, and indicate
the angle  by a red arc:



We find the value of r (the hypotenuse) by the Pythagorean theorem:









r is always positive so we take the positive square root:




We find  by using any trig function, say the cosine;
cos(theta)=adjacent/hypotenuse=x/r=sqrt(3)/2}}}

This tells us that the angle has a refence angle of 30°, but since
it is in quadrant IV, we subtract from 360° and get 




Next we know that

, so 

Also, we know that

, so 

So 

x + iy = 2·cos(330°)+i·2·sin(330°) = 2[cos(330°) + i·sin(330°)]

Edwin