Find the roots of z^6=1 for z complex. Show that the sum of the roots you found is zero.
 Get 0 on the right:
Get 0 on the right:
 Write as the difference of two squares:
Write as the difference of two squares:
 Factor as the difference of squares:
Factor as the difference of squares:
 Write the first factor as the difference of two cubes
and the second factor as the sum of two cubes:
Write the first factor as the difference of two cubes
and the second factor as the sum of two cubes:
 Factor each by the rule for factoring the difference
(and sum) of two cubes
Factor each by the rule for factoring the difference
(and sum) of two cubes
 Set each factor = 0
Set each factor = 0
 yields root
yields root 
 yields root
yields root 
 , by the quadratic formula
yields roots
, by the quadratic formula
yields roots  and
and 
 , by the quadratic formula
yields roots
, by the quadratic formula
yields roots  and
and  .
------------------------------
So the 6 roots are:
.
------------------------------
So the 6 roots are:
 ,
,  ,
,  ,
,  ,
, 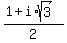 ,
, 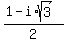 Add them up:
Add them up:
 =
=
 =
=  Edwin
Edwin