SOLUTION: If 1 and w are two of the five roots of w^5=1, then show that w^2, w^3 and w^4 are the remaining roots of w^5=1.

Algebra ->  Complex Numbers Imaginary Numbers Solvers and Lesson -> SOLUTION: If 1 and w are two of the five roots of w^5=1, then show that w^2, w^3 and w^4 are the remaining roots of w^5=1.       Log On


   

Question 1160400: If 1 and w are two of the five roots of w^5=1, then show that w^2, w^3 and w^4 are the remaining roots of w^5=1.
Answer by ikleyn(52803) About Me  (Show Source):
You can put this solution on YOUR website!
.

Let me start teaching you how to formulate this problem CORRECTLY. 

    the number  " 1 "  highlight%28IS%29 the root of the equation w^5 = 1.

    Therefore, there is no need to write  "if 1 and w are two of the five roots of w^=1.



             (otherwise, it makes very strange impression).




    The correct writing is "if w is the root of the equation w^5 = 1, different from 1 . . . and so on . . . ".


Now to the solution. 

If w is the root of the equation w^5 = 1, then


    %28w%5E2%29%5E5 = w%5E%282%2A5%29 = %28W%5E5%29%5E2 = 1%5E2 = 1,

    so w%5E2  is the root of the same equation.



Same proof works for  w%5E3.


    %28w%5E3%29%5E5 = w%5E%283%2A5%29 = %28W%5E5%29%5E3 = 1%5E3 = 1,

    so w%5E3  is the root of the same equation.



Same proof works for  w%5E4.

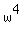Do it on your own, as a useful exercise.

-------------

Proved and solved. And completed.