Question 1083651: How would you write  in standard form
Found 2 solutions by Edwin McCravy, rothauserc:
Answer by Edwin McCravy(20056)   (Show Source):
You can put this solution on YOUR website!
Let   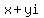, where x and y are real.
Since complex imaginary numbers are neither positive nor
negative, there is no rule about using the radical with
complex imaginary numbers as there is for real numbers.
So I suppose they want both square roots of 3-4i.
square both sides
 
Equate real parts:
Equate imaginary parts:
Solve the system of equations:
Solve the second for y and substitute in the first,
and solve for the real soultions for x, then substitute
in one of the equations to get the real solutions for y.
At first there are four potential solutions:
2+i, 2-i, -2+i, -2-i.
However, to check for extraneous answers, we find that
by squaring each of them, we find that only 2-i and -2+i
are solutions.
Edwin
Answer by rothauserc(4718)  (Show Source):
You can put this solution on YOUR website! standard form of a complex number is a + bi, where a and b are real numbers and i is the square root(-1)
:
sqrt(3 - 4i) = a+bi
:
square both sides of =
:
3 - 4i = (a+bi)^2
3 - 4i = (a^2 + 2abi -b^2)
:
we have two equations in two unknowns
:
1) 3 = a^2 - b^2
2) -4i = 2abi
:
solve equation 2 for a
:
a = -4i / 2bi = -2/b
:
substitute for a in equation 1 and solve for b
:
b^4 +3b^2 -4 = 0
:
let u = b^2, then
:
u^2 +3u -4 = 0
:
factor polynomial
:
(u+4) * (u-1) = 0
:
u = -4 and u = 1
:
b^2 = -4 and b^2 = 1
:
b = 2i, -2i, 1, -1, b is real so reject 2i and -2i
:
a = -2/b
:
a = -2 or 2
:
********************************
standard form is 2 - i or -2 + i
********************************
:
|
|
|
