Question 1032243: 1. Create different sets of expressions that satisfy each desired outcome:
a. Find a pair of complex binomials whose sum is 8 + 9i.
b. Find a pair of complex binomials whose difference is -2 + 6i.
2. Make a generalization about the exponents of imaginary numbers, regarding whether or not all even or all odd exponents result in real or imaginary numbers. Explain and prove your statement with actual examples and at least one complete sentence that supports your generalization.
(Note: Please show all work so that I can understand your logic. Thank you)
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! 1.a.
 and and  are two (a pair of) complex binomials that add up to are two (a pair of) complex binomials that add up to  . .
     is an option is an option
because  and and  . .
     is an option is an option
because  and and  . .
The possibilities are endless. All we have to do is find a pair of real numbers that add up to  for the first term of the two complex binomials, and another pair of real numbers that add up to for the first term of the two complex binomials, and another pair of real numbers that add up to  for the coefficients of for the coefficients of  of the two complex binomials. of the two complex binomials.
THE LOGIC:
 and and  are two binomials that add up to are two binomials that add up to  . .
Those binomials include the (unknown) variable  , ,
and unless told otherwise we think of  as a real number. as a real number.
Placing the imaginary number  in the spot where the variable in the spot where the variable  was does not change the way we add or subtract. (In math, new definitions are crafted so as to change the way we operate as little as possible. That way, fractional exponents, complex numbers, and the like do not cause us much trouble). was does not change the way we add or subtract. (In math, new definitions are crafted so as to change the way we operate as little as possible. That way, fractional exponents, complex numbers, and the like do not cause us much trouble).
1.b.  and and  are two (a pair of) complex binomials whose difference is are two (a pair of) complex binomials whose difference is  . .
 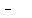    is an option is an option
As for the sum, the possibilities for the difference are endless. All we have to do is find a pair of real numbers whose difference is  for the first term of the two complex binomials, and another pair of real numbers whose difference is for the first term of the two complex binomials, and another pair of real numbers whose difference is  for the coefficients of for the coefficients of  of the two complex binomials. of the two complex binomials.
2. The definition of an imaginary number is usually a complex number like  , or , or 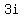 , or , or  . .
"Make a generalization" and "Explain and prove your statement with actual examples and at least one complete sentence" suggest that you are expected to try examples with different odd and even exponents, and maybe even different imaginary numbers until you come up with an "experimental" generalization.
STATEMENT: Powers of imaginary numbers are real whenever the exponent is even, and imaginary whenever the exponent is odd.
EXAMPLES, "PROOF" AND COMPLETE SENTENCES:
 is real, and is real, and
 , ,
just like  . .
 is imaginary, is imaginary,
just like  is imaginary. is imaginary.
So, the coefficient of  could be could be  or or  or any real number, or any real number,
but it makes no difference,
because the power is real when the same power of  is real, is real,
and the power is imaginary when the same power of  is imaginary. is imaginary.
 and and  Powers of Powers of  with an even exponent can be written as powers of with an even exponent can be written as powers of  , which is a real number, and that makes them real numbers. , which is a real number, and that makes them real numbers.
 and and 
Powers of  with an odd exponent can be written as powers of with an odd exponent can be written as powers of  with an even exponent times with an even exponent times  , and since the power with an even exponent is real, its product time , and since the power with an even exponent is real, its product time  is imaginary. is imaginary.
NOTES:
Hopefully the teacher would be satisfied with that. Sometimes it is hard to know what kind of answer is expected.
I do not know if you will understand my logic, but I understand why someone would need help with this problem. This problem may have been created by someone who believes math is an experimental science. I do not agree, but all kinds of beliefs are allowed.
Or maybe the idea is that some students need to work with concrete examples, before generalizing to abstract concepts.
Either way, if you are an abstract thinker, you will find this problem annoying, but humoring the teacher is often the best strategy.
|
|
|