Question 1116383: Find the set of values of x which satisfies each of the following inequalities.
a) |x - 2| > x + |x|,
b) |4x - 1| > x - 2
Found 3 solutions by josgarithmetic, ikleyn, greenestamps:
Answer by josgarithmetic(39620)   (Show Source):
Answer by ikleyn(52810)  (Show Source):
You can put this solution on YOUR website! .
Nothing is as far from the correct solution as this writing by @josgarithmetic.
-------------------------------
a) |x - 2| > x + |x|
It is an absolute value inequality.
The method of solving such inequalities is to divide the number line in intervals where each term of the equation is a linear function,
and then solve the resulting inequalities for linear functions for each separate interval.
In this case the critical values, where functions change their behavior, are x= 0 and x= 2. They divide the number line
in three intervals: 1) x < 0; 2) 0 < x < 2, and 3) x > 2.
Plot y =  (red) and y = x + abs(x) (green)
In the FIRST interval, x < 0, we have (x-2) < 0; therefore |x-2| = -(x-2).
Also, in this interval x < 0, therefore |x| = -x and then x + |x| = x + (-x) = 0.
Thus in the first interval the inequality takes the form
-(x-2) > 0 , or, equivalently,
x - 2 < 0, or
x < 2, which is always TRUE in the interval x < 0.
Thus the first interval, x < 0, is the part of the solution to the original inequality.
At this point I completed with the first interval and now start working with the second interval.
In the SECOND interval, 0 < x < 2, we have (x-2) < 0; therefore |x-2| = -(x-2).
Also, in this interval x > 0, therefore |x| = x, and then x + |x| = x + x = 2x.
Thus in the second interval the inequality takes the form
-(x-2) > 2x , or, equivalently,
2x + (x - 2) < 0, or
3x < 2, which is TRUE if x <  .
Thus for the second interval, 0 < x < 2, ONLY PART OF IT x < is the solution to the original inequality.
In the THIRD interval, x > 2, we have (x-2) > 0; therefore |x-2| = (x-2).
Also, in this interval x > 0, therefore |x| = x, and then x + |x| = x + x = 2x.
Thus in the third interval the inequality takes the form
(x-2) > 2x , or, equivalently,
2x - (x - 2) < 0, or
x < 2, which is always FALSE in the interval x > 2.
Thus for the third interval, x > 2. NO PART OF IT is the solution to the original inequality.
After this analysis you can conclude that the solution set to the original inequality is x <  , or, in interval form, ( ,).
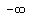Answer. The solution set to the original inequality is x < , or, in interval form, (,).
----------------
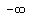If you want to see other similar solved problems on absolute value inequalities, look into the lessons
- Absolute Value equations
- HOW TO solve equations containing Linear Terms under the Absolute Value sign. Lesson 1
- HOW TO solve equations containing Linear Terms under the Absolute Value sign. Lesson 2
- HOW TO solve equations containing Linear Terms under the Absolute Value sign. Lesson 3
- HOW TO solve equations containing Quadratic Terms under the Absolute Value sign. Lesson 1
- HOW TO solve equations containing Quadratic Terms under the Absolute Value sign. Lesson 2
- OVERVIEW of lessons on Absolute Value equations
Read them attentively and become an expert in this area.
Also, you have this free of charge online textbook in ALGEBRA-I in this site
- ALGEBRA-I - YOUR ONLINE TEXTBOOK.
The referred lessons are the part of this online textbook under the topic
"Solving Absolute values equations".
Save the link to this online textbook together with its description
Free of charge online textbook in ALGEBRA-I
https://www.algebra.com/algebra/homework/quadratic/lessons/ALGEBRA-I-YOUR-ONLINE-TEXTBOOK.lesson
to your archive and use it when it is needed.
===============
I think that these sources are the only place in the american school math literature, where you can learn the subject adequately.
Answer by greenestamps(13202)  (Show Source):
You can put this solution on YOUR website!
In the first inequality, there are two absolute value expressions, so we have to consider different cases when x is positive or negative and when x-2 is positive or negative. So we have three intervals on the number line to consider: from negative infinity to 0; from 0 to 2, and from 2 to infinity.
The right side of the inequality makes the first interval easy. For negative values of x,  . The inequality then says that some absolute value is greater than 0, which is always true.
So all negative numbers are part of the solution set of the inequality.
Between 0 and 2,  so the inequality says
So, of the x values between 0 and 2, the ones that satisfy the inequality are those less than 2/3.
For the interval from 2 to infinity,  and the inequality says
But this apparent solution is not in the interval we are working in. So no values of x in the interval from 2 to infinity satisfy the inequality.
So our final solution set is from negative infinity to 2/3, not including 2/3.
The second inequality is a bit easier, because there is only one absolute value expression.  is equal to 4x-1 for x values greater than or equal to 1/4, or equal to 1-4x for x values less than 1/4. So
(a) for x < 1/4,
ALL values of x that are less than 1/4 are less than 3/5; so all values of x less than 1/4 are solutions to the inequality.
(b) for x > 1/4,
Again, all values of x that are greater than 1/4 are greater than -1/3.
So every value of x is a solution to the second inequality.
This is easily verified with even a rough sketch of the graphs of the two expressions:
The value of the absolute value expression is always greater than the value of the linear expression.
|
|
|
