|
This Lesson (Volume of pyramids) was created by by ikleyn(52787)   : View Source, ShowAbout ikleyn:
Volume of pyramids
Pyramid is a 3D solid body with flat faces which has one distinguished face of a polygonal shape, while all other faces are of a triangular shape with a common vertex for all triangles. The distinguished face is called the pyramid base. The remaining faces are called the lateral faces. The lateral faces are of triangular form.
Structurally a pyramid can be thought as a polygon on a plane and a point in a space out of the plane, which is connected with the polygon vertices by straight line segments - the edges of the pyramid. Figures 1a - 1e present the examples of pyramids.

Figure 1a. Rectangular pyramid
|

Figure 1b. Rectangular pyramid
|

Figure 1c. Triangular pyramid
|

Figure 1d. Triangular pyramid
|

Figure 1e. Hexagonal pyramid
|
The base of a pyramid can be any type of polygon. Depending on the shape of this polygon, the prism can be called a triangular prism, or rectangular prism, or pentagonal, hexagonal and so on.
The height of a pyramid (sometimes called the altitude of a pyramid) is
the perpendicular segment from the vertex, located out of the base plane, to
the base (Figures 2a and 2b).
If the polygon at the base of a pyramid is regular and all the pyramid lateral
edges have the same length then the pyramid is called a regular pyramid.
In a regular pyramid the altitude drops to the center of the regular polygon at
the base. In other words, in a regular pyramid the foot of the altitude
coincides with the center of the regular polygon at the base.
This lesson is focused on calculating the volume of pyramids.
|

Figure 2a. The height
of a pyramid
|

Figure 2b. The height
of a pyramid
|
Formula for calculating the volume of pyramids
The volume of a pyramid is  = =   . . , ,
where  is the area of the base of the pyramid and is the area of the base of the pyramid and  are the pyramid's height. are the pyramid's height.
|
Example 1Find the volume of a regular pyramid with the square base (Figure 3) if the height of the pyramid is of 12 cm and the measure of the base edge is of 10 cm.
Solution
The area of the base of the given pyramid is
 = = 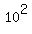 = 100 = 100  . .
Hence, the volume of the pyramid is   . . = 400 = 400  . .
Answer. The volume of the pyramid is 400  . .
|

Figure 3. To the Example 1
|
Example 2Find the volume of a regular pyramid with the square base (Figure 4a) if the lateral edge of the pyramid has the same measure of 12 cm as the the base edge has.
Also find the angle between the lateral edge and the base of the pyramid.
Solution
First, let us find the area of the base of the given pyramid.
Since the base is a square with the side measure of 12 cm, the area of the base is
 = =  = 144 = 144  . .
Next, let us find the height of the pyramid.
For it, let us consider the triangle  AOP (Figure 4b), where the point A is one AOP (Figure 4b), where the point A is one
of the base vertices of the pyramid, the point O is the center of the square base
of the pyramid, and the point P is the pyramid vertex.
It is a right-angled triangle (the segment OP is the height of the pyramid). Its
leg AO is half of the diagonal of the square base, and its measure is  = = 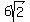 . .
Therefore, the measure of the height OP is
|OP| =  = =  = =  = =  = = 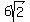 cm. cm.
|

Figure 4a. To the Example 2
|

Figure 4b. To the solution
of the Example 2
|
Now, the volume of the given pyramid is  = =   . .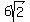 = =  = 407.29 = 407.29  (approximately). (approximately).
On the way, we proved that the right-angled triangle  AOP is isosceles: |OP| = |AO|. AOP is isosceles: |OP| = |AO|.
It means that the angle LOAP is of 45°.
Answer. The volume of the given pyramid is  = =   (approximately). (approximately).
The angle between the lateral edge and the base of the pyramid is of 45°.
Example 3Find the volume of a regular hexagonal pyramid if its base edge is of 4 cm and the height of the pyramid is of 6 cm (Figure 5).
Solution
First, let us find the base area of the pyramid.
Since the base is a regular hexagon, its area is
 = =  *( *( . . . .  ) = ) =    . .
Now, the volume of the pyramid is
 = =   . . = =  . .  . . = =   = =  * * = 83.138 = 83.138  (approximately). (approximately).
Answer. The volume of the pyramid is 83.138  (approximately). (approximately).
|

Figure 5. To the Example 3
|
Example 4Find the volume of a regular tetrahedron if all its edges are of 10 cm long (Figure 6a).
Solution
The base area of the given tetrahedron is the area of the equilateral triangle with the
side measure of 10cm. So, the base area is equal to  = =  . . . .  = =   . .
Next, let us find the measure of the height of the given tetrahedron (Figure 6b).
The height OP of the given tetrahedron drops to the center O of its base, which
is the intersection point of the base altitudes, medians and angle bisectors.
It is well known fact of Planimetry that the intersection point of medians of a
triangle divides them in proportion 2:1 counting from the vertices (see the lesson
Medians of a triangle are concurrent in this site).
Thus the segment OA in Figure 6b has the length of two third of the altitude
of the base triangle, i.e. |OA| =  . .  = =  . .
|

Figure 6a. To the Example 4
|

Figure 6b. To the solution
of the Example 4
|
Now, the height of the pyramid is  = =  = =  = =  = =  , ,
and the volume of our tetrahedron is  = =  . . . . = =  . .  . . = =  = =  = 117.85 = 117.85  (approximately). (approximately).
Answer. The volume of the given tetrahedron is  = 117.85 = 117.85  (approximately). (approximately).
(I intentionally presented the answer via the dimension of the tetrahedron's edge).
The general formula for the volume of a regular tetrahedron with the edge size  is is  . You can prove this formula yourself using the same arguments). . You can prove this formula yourself using the same arguments).
Example 5Find the volume of a composite solid body of a "diamond" shape which comprises of two regular tetrahedrons joined face to face (Figure 7), if all their edges are
of 4 cm long.
Solution
We are given a 3D body of a "diamond" shape comprised of two regular tetrahedrons
whose two faces are joined and overposed each to the other (Figure 7).
The total volume of our solid body is twice the volume of the single regular
tetrahedron with the side measure of 4 cm. The later is equal to
 , according to the solution of the Example 4 above. , according to the solution of the Example 4 above.
Thus the volume of the composite body under consideration is
 . . = =  = =  = 15.085 = 15.085  (approximately). (approximately).
|

Figure 7. To the Example 5
|
Answer. The volume of the composite body under consideration is  . . = 15.085 = 15.085  (approximately). (approximately).
Example 6Find the volume of a body obtained from the regular tetrahedron with the edge measure of 10 cm after cutting off the part of the tetrahedron by the plane parallel to one of its faces in a way that the cutting plane bisects the three edges of the original tetrahedron (truncated tetrahedron, Figure 7).
Solution
The strategy solving this problem is to find first the volume of the regular tetrahedron
with the edge measure of 10 cm and then to distract the volume of the regular
tetrahedron with the edge measure of 5 cm.
The volume of the original regular tetrahedron was found in the solution of the Example 4
above. It is equal to  = 117.85 = 117.85  (approximately). (approximately).
The volume of the smaller regular tetrahedron with the edge size of 5 cm can be found using
similar formula with replacing the value of the edge size of 10 cm by 5 cm.
So, the volume of the smaller tetrahedron is  = 14.73 = 14.73  (approximately). (approximately).
|

Figure 7. To the Example 5
|
Now, the volume of the truncated tetrahedron is 117.85 - 14.73 = 103.12  (approximately). (approximately).
Answer. The volume of the body under consideration (truncated regular tetrahedron) is  - -  = 103.12 = 103.12  (approximately). (approximately).
My lessons on volume of pyramids and other 3D solid bodies in this site are
To navigate over all topics/lessons of the Online Geometry Textbook use this file/link GEOMETRY - YOUR ONLINE TEXTBOOK.
This lesson has been accessed 7170 times.
|
| |

