SOLUTION: The areas Of the faces Of a right rectangular prism are 6, 9, and 12cm^2. a, To the nearest tenth of a centimeter, what is the length of the diagonal of the prism? b, what is th

Algebra ->  Volume -> SOLUTION: The areas Of the faces Of a right rectangular prism are 6, 9, and 12cm^2. a, To the nearest tenth of a centimeter, what is the length of the diagonal of the prism? b, what is th      Log On


   

Question 1181236: The areas Of the faces Of a right rectangular prism are 6, 9, and 12cm^2.
a, To the nearest tenth of a centimeter, what is the length of the diagonal of the prism?
b, what is the volume of the prism? Anser in simplest radical form
Answer by ikleyn(52806) About Me  (Show Source):
You can put this solution on YOUR website!
.

            As the problem is worded and presented,  it is  TERRIBLE.

            Nevertheless,  I was able to decipher its hidden meaning.

            So,  I will solve the problem,  but do not ask me how I guessed my interpretation. 


Let x, y and z be the three dimensions of the prism.

Then we are given these three equations


    xy = 6    (1)

    xz = 9    (2)

    yz = 12   (3)


Multiply these equations. You will get


    (xyz)^2 = 6*9*12 = 648 = (2*3) * (3*3) * (3*4) = 2 * 3^4 * 4 = 2^3 * 3^4


which implies

     xyz = sqrt%28648%29 = sqrt%282%5E3%2A3%5E4%29 = 2%2A3%5E2%2Asqrt%282%29 = 18%2Asqrt%282%29.    (4)



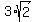Now       divide equation (4) by equation (1).  You will get  z = %2818%2Asqrt%282%29%29%2F6 = 3%2Asqrt%282%29.


Next,     divide equation (4) by equation (2).  You will get  y = %2818%2Asqrt%282%29%29%2F9 = 2%2Asqrt%282%29.


Finally,  divide equation (4) by equation (3).  You will get  x = %2818%2Asqrt%282%29%29%2F12 = %283%2F2%29%2Asqrt%282%29.


       +-----------------------------------------------------+
       |   So, at this point we know all the dimensions,     | 
       |   and now I am ready answer the questions.          |
       +-----------------------------------------------------+



(a)  To the nearest tenth of a centimeter, what is the length of the diagonal of the prism?


         The square of the diagonal length is  d^2 = x^2 + y^2 + z^2 = %289%2F4%29%2A2+%2B+4%2A2+%2B+9%2A2 = 38.5;

         hence, the diagonal is  d = sqrt%2838.5%29 = 6.2 cm  (rounded).      ANSWER



(b)  What is the volume of the prism?


         The volume is  V = xyz = 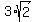%283%2F2%29%2Asqrt%282%29.2%2Asqrt%282%29.3%2Asqrt%282%29 = %283%2F2%29%2A2%2A3%2A2%2Asqrt%282%29 = 18%2Asqrt%282%29 = 25.456 cm^3  (rounded).    ANSWER

The problem is solved.

All the questions are answered.

You get a brilliant solution with the careful explanation.


//////////////


Do not forget to post your  "THANKS"  to me for my teaching.