SOLUTION: Find the area of the triangle formed by x and y axis and the tangent line to {{{ f(x) = 1/x^2 }}} at points ( 3, f(3) )

Algebra ->  Trigonometry-basics -> SOLUTION: Find the area of the triangle formed by x and y axis and the tangent line to {{{ f(x) = 1/x^2 }}} at points ( 3, f(3) )      Log On


   

Question 909276: Find the area of the triangle formed by x and y axis and the tangent line to
+f%28x%29+=+1%2Fx%5E2+ at points ( 3, f(3) )
Answer by josgarithmetic(39617) About Me  (Show Source):
You can put this solution on YOUR website!
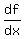df%2Fdx=%28d%2Fdx%29%28x%5E-2%29
df%2Fdx=-2x%5E-3
-
df%2Fdx at 3 is -2%2A%283%29%5E-3=-2%2F27.
Line containing that slope and (3,f(3)) is y-f%283%29=-%282%2F27%29%28x-3%29
y-%281%2F9%29=-%282%2F27%29%28x-3%29
y-1%2F9=-%282%2F27%29x%2B2%2F9
y=-%282%2F27%29x%2B1%2F3------One point is obviously (0, 1/3) and another would be (0,0).

Use the linear equation to find the x-axis intercept (when y=0).

0=-%282%2F27%29x%2B1%2F3
%282%2F27%29x=1%2F3
x=%2827%2F2%29%281%2F3%29
x=9%2F2-------The point being, ( 9/2, 0 ).

SUMMARY:
The triangle's points are ( 0,0 ), ( 9/2, 0 ), and ( 0, 1/3 ).
Finish the area calculation.