SOLUTION: Use the trigonometric function values of the quadrant angles to evaluate. 7 cot 270 degrees + 3 cos 180 degrees.

Question 898836: Use the trigonometric function values of the quadrant angles to evaluate.
7 cot 270 degrees + 3 cos 180 degrees.
Answer by Theo(13342) (Show Source): You can put this solution on YOUR website!
7*cot(270) = 0

3*cos(180) = -3

7*cot(270) - 3*cos(180) is equal to 0 + 3 which is equal to 3.

that's your solution.

i used a calculator.
if i didn't have a calculator, i would do the following.

reference angle for 270 degrees is equal to 90 because 180 + 90 = 270.
cot(90) = cos(90)/sin(90) = 0/1 = 0.
cot(90) = 0
270 is in between the third and fourth quadrant.
since the cotangent is equal to 0, the sign doesn't matter, so cot(270) = 0.

reference angle for 180 is equal to 0 because 180 - 180 = 0.
cos(0) = 1
180 degrees is between second and third quadrant.
cosine is negative when the angle is in between the second and third quadrant, so cos(180) = -1

therefore:

7*cot(270) - 3*cos(180) = 7*0 - 3*(-1) which is equal to 0 + 3 which is equal to 3.

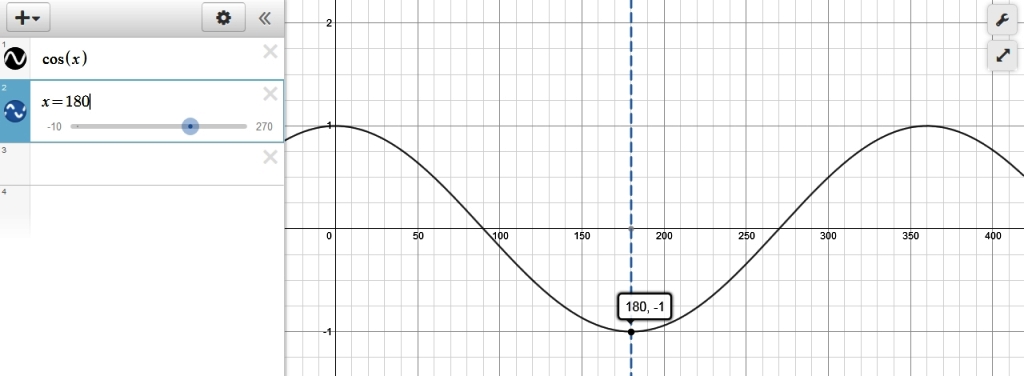
the graphs of cot(270) and cos(180) are shown below:

$$$

RELATED QUESTIONS
the question is: Find the exact value of the remaining trigonometric functions if: tan... (answered by josmiceli,solver91311)

find the trig. ratio of the following cot 180(degrees) csc -270(degrees) sec... (answered by venugopalramana)

Evaluate sin 0 degrees+cos 180 degrees-sin 270... (answered by stanbon,solver91311)

Use the given information to determine the exact trigonometric value. If csc(theta)=... (answered by stanbon)

Use the given information to determine the exact trigonometric value. If cos(theta)=4/5... (answered by stanbon)

cos theta= -1/3 and 180 degrees < theta < 270 degrees find the exact values of sin... (answered by Alan3354)

Use trigonometrical identities to expand and simplify if possible, the following: 1) cos (answered by swincher4391)

Which of the following contains a false solution to the equation sinθ... (answered by Edwin McCravy)

Express each as a trigonometric function of a reference angle and give the value to 4... (answered by stanbon)