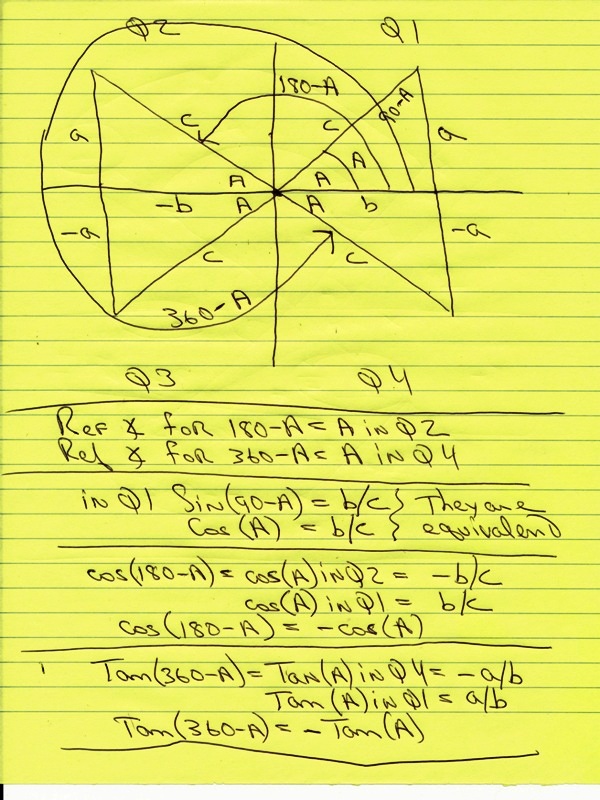
cos(180-x) = -cos(x)
tan(360-x) = -tan(x)
use these basic formulas to get your simplified expression.
Start with:
Sin(90-x)tan(360-x)/Cos(180-x)
Replace sin(90-x) with cos(x)
Replace cos(180-x) with -cos(x)
Replace tan(360-x) with -tan(x)
You get:
cos(x)*-tan(x)/-cos(x)
cos(x)/-cos(x) = -1
Expression becomes:
-1*-tan(x)
-1*-1 = 1
Expression becomes:
tan(x)
That's your answer.
Sin(90-x)tan(360-x)/Cos(180-x) = tan(x).
Take any angle and replace x with it and you'll see that the equivalency is correct.
Example:
x = 60 degrees (chosen at random)
sin(90-x) = sin(90-60) = sin(30) in quadrant 1 = .5
cos(180-x) = cos(180-60) = cos(120)= cos(60) in quadrant 2 = -.5
tan(360-x) = tan(360-60) = tan(300) = tan(60) in quadrant 4 = -1.73205
sin(90-x)*tan(360-x)/cos(180-x) = .5*-1.73205/-.5 = 1.73205
tan(60) = 1.73205
Answers are the same, therefore:
sin(90-x)*tan(360-x)/cos(180-x) = tan(x)
The reference angle for all of the angles greater than 90 degrees is equal to 60 degrees.
cos(120) = cos(180-60) therefore 60 is the reference angle in quadrant 2.
tan(300) = tan(360-60) therefore 60 is the reference angle in quadrant 4.
for the angle less than 90 degrees, the standard right triangle shows that:
sin(90 - 60) = sin(30) = .5 = cos(90 - 30) = cos(60) = .5
In the different quadrants, the relationships are shown in the following diagram:
A good reference that talks about reference angles can be found here:
http://www.mathwarehouse.com/trigonometry/reference-angle/finding-reference-angle.php