SOLUTION: Find the exact value of the expression. sin(cos^-1 2/3 - tan^-1 1/4)

Algebra ->  Trigonometry-basics -> SOLUTION: Find the exact value of the expression. sin(cos^-1 2/3 - tan^-1 1/4)      Log On


   

Question 871093: Find the exact value of the expression.
sin(cos^-1 2/3 - tan^-1 1/4)
Answer by KMST(5328) About Me  (Show Source):
You can put this solution on YOUR website!
NOTE: I am rushing to get done before I have to go to my day job, so check for mistakes.

In this problem "cos^-1" means the inverse function of cosine,
and "tan^-1" means the inverse function of tangent.
We are looking for the exact value of
sin%28A-B%29 knowing that cos%28A%29=2%2F3 and tan%28B%29=1%2F4,
and that those inverse functions are defined so that
A will be in quadrants I or II, and
B will be in quadrants I or IV.

To calculate sin%28A-B%29 we can use the trigonometric identity
sin%28A-B%29=sin%28A%29%2Acos%28B%29-sin%28B%29%2Acos%28A%29
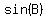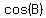So we need to find sin%28A%29 , sin%28B%29 , and cos%28B%29 .

In quadrants I and I sin%28A%29%3E0, so


Since tan%28B%29=1%2F4%3E0 only hapens in quadrants I and III,
and the definition of the inverse tangent function says that B is in I or IV,
B is definitely in quadrant I, where sine and cosine are positive.
This is how angle B would look in a right triangle.
The hypotenuse of that right triangle measures sqrt%284%5E2%2B1%5E2%29=sqrt%2816%2B1%29=sqrt%2817%29
So, sin%28B%29=1%2Fsqrt%2817%29 and cos%28B%29=4%2Fsqrt%2817%29
Substituting all the values found into sin%28A-B%29=sin%28A%29%2Acos%28B%29-sin%28B%29%2Acos%28A%29 ,

SInce that does not look elegant, and teachers do not like square roots in denominators, we multiply numerator and denominator times sqrt%2817%29 to get