SOLUTION: prove the co-function identity tan(x+ pi/2) = -cotx

Question 870083: prove the co-function identity tan(x+ pi/2) = -cotx
Answer by Theo(13342) (Show Source): You can put this solution on YOUR website!
it is given that:

cot(x) = tan(90 - x)

this assumes both your angles are in quadrant 1.

you have angle x and you have angle 90 - x.

the equivalent angles in the second quadrant are (180 - x) and (180 - (90 - x)).

the reference angle for (180 - x) is equal to x.

the reference angle for (180 - (90 - x)) is equal to 90 - x).

since (180 - x) is in quadrant 2, then tan(180 - x) = -tan(x) and cot(180 - x) = -cot(x).

since 180 - (90 - x) is in quadrant 2, then tan(180 - (90 - x)) = -tan((90 - x) and cot(180 - (90 - x) = -cot(90 - x).

we'll start with:

cot(180 - x) = tan(180 - (90 - x))

this is true because the reference angle for (180 - x) is x and the reference angle for (180 - (90 - x)) is (90 - x) and we already know that cot(x) = tan(90 - x).

we also know that cot(180 - x) is equal to -cot(x) because the cotangent function in the second quadrant is the negative of the cotangent function in the first quadrant for the angles that have the same reference angle. since the reference angle for (180 - x) is x, this rule applies.

our equation therefore becomes:

-cot(x) = tan(180 - (90 - x))

we can simplify tan(180 - (90 - x) to be equivalent to tan (90 + x).

this completes the proof.

-cot(x) = tan(90 + x) which is the same as:

tan(90 + x) = -cot(x).

a picture of the angles in quadrants 1 and 2 is shown below:

$$$

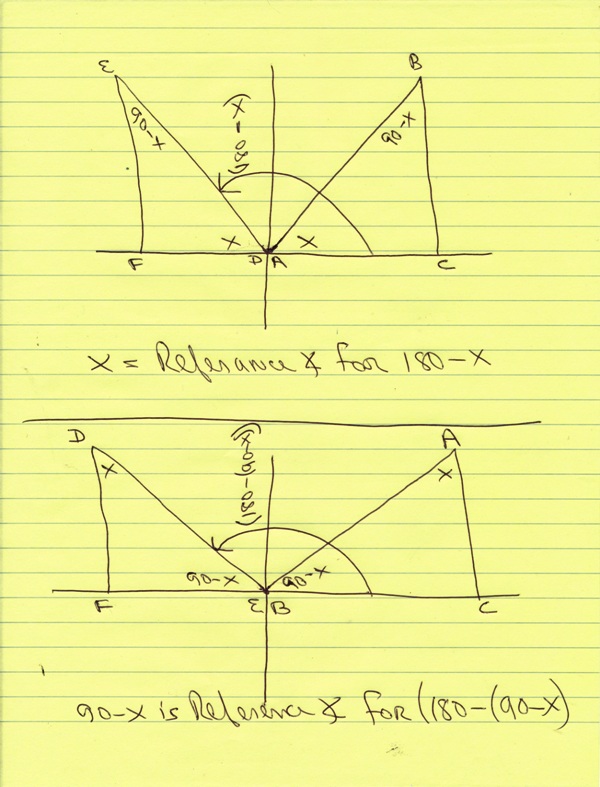
in the picture, the same triangle has been turned around so you can see that the same rule applies to both angle x and angle (90 - x).

RELATED QUESTIONS
Prove that... (answered by jim_thompson5910)

prove using the t = tan (x/2) [tan 2x + cotx] / [tan2x - tanx] - cot^2... (answered by ikleyn)

Verify the identity.... (answered by lwsshak3)

Verify the identity. cot (x- (pi/2)) = -tan... (answered by Boreal)

Prove the identity: Sin2x (tan x + cot x) = 2... (answered by lwsshak3)

Prove that the identity is true {{{ tan(x)^3= tan(x)sec(x)^2-tan(x)... (answered by lwsshak3)

Prove the identity: Tan^2(x)-sin^2(x)... (answered by Fombitz)

Prove the identity: Tan^2(x)/(1+tan^2(x)) =... (answered by Theo)

Prove the identity: {{{tan(x) /( 1 + (tan(x))^2) = sin(x)cos(x)}}} (x is... (answered by jim_thompson5910)